题目内容
1.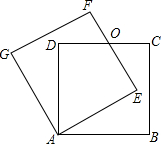 如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O
如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O(1)以图中标有字母的点为端点连接两条线的(正方形的对角线除外),要求所连接的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为2cm,若旋转的角度为30°,求重叠部分(四边形AEOD)的面积.
分析 (1)连接OE、AO,证明△ADO≌△AEO,从而可证明AO是DE的垂直平分线;
(2)△ADO中,根据特殊锐角三角函数值求得OE的长,然后利用三角形的面积公式求解即可.
解答 解:(1)如图所示连接OE、AO.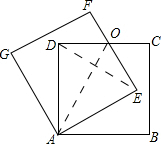
由正方形的性质和旋转的性质可知:AD=AE,∠CDA=∠AEF=90°,
在Rt△ADO和Rt△AEO中,
$\left\{\begin{array}{l}{AD=AE}\\{AO=AO}\end{array}\right.$,
∴Rt△ADO≌Rt△AEO.
∴OD=OE.
∵AD=AE,OD=EO,
∴AO是DE的垂直平分线.
∴AO⊥DE.
(2)∵旋转的角度为30°,
∴∠EAN=30°.
∴∠DAE=60°.
由(1)可知:Rt△ADO≌Rt△AEO,
∴∠OAE=$\frac{1}{2}∠DAE$=30°.
∴$\frac{OE}{AE}=\frac{\sqrt{3}}{3}$.
∴OE=$\frac{\sqrt{3}}{3}×2$=$\frac{2\sqrt{3}}{3}$.
∴重合部分的面积=2SAOE=2×$\frac{1}{2}×2×\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查的是正方形的性质、旋转的性质、全等三角形的性质和判定,证得Rt△ADO≌Rt△AEO是解题的关键.

练习册系列答案
相关题目
11.顺次连结对角线垂直的四边形各边中点,所得四边形是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 任意四边形 |
9.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AC⊥BD |
16.一元二次方程x2+3=2$\sqrt{3}$x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的有理根 | ||
| C. | 有两个相等的无理根 | D. | 没有实数根 |