题目内容
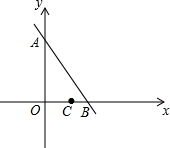 如图,已知点A(0,6),B(3,0),C(2,0).设点M的坐标为(0,m),其中m<6,以M为圆心,MC为半径作圆.
如图,已知点A(0,6),B(3,0),C(2,0).设点M的坐标为(0,m),其中m<6,以M为圆心,MC为半径作圆.(1)当m=0时,⊙M与直线AB的位置关系是
当m=3时,⊙M与直线AB的位置关系是
(2)当⊙M与直线AB相切时,m的值为
(3)直接写出m在什么范围内取值时,⊙M与直线AB相交、相离.
考点:直线与圆的位置关系,坐标与图形性质
专题:
分析:(1)代入m的值,求得MC的长,然后与圆心到AB的距离大小比较后即可确定圆与直线的位置关系;
(2)根据已知,连接MN、MB、MC,则MN⊥AB,首先利用等积法求得线段MN的长,根据相切时MN=MC列出等式求得m的值即可;
(3)根据(2)求得的结果写出答案即可.
(2)根据已知,连接MN、MB、MC,则MN⊥AB,首先利用等积法求得线段MN的长,根据相切时MN=MC列出等式求得m的值即可;
(3)根据(2)求得的结果写出答案即可.
解答:解:(1)当m=0时,⊙M与直线AB的位置关系是相离;
当m=3时,⊙M与直线AB的位置关系是相交;
(2)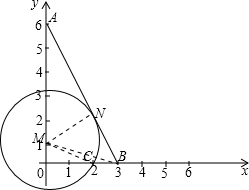 连接MN、MB、MC,则MN⊥AB,
连接MN、MB、MC,则MN⊥AB,
在Rt△ABO中,AB2=OA2+OB2,AB=
=3
,
在△AMB中,S△AMB=
AB•MN=
AM•OB,
∴MN=
=
=
,
在Rt△OMC中,MC2=OM2+OC2,OM2=m2+4,
∵MN、MC均为⊙M的半径,
∴MN=MC,(
)2=m2+4,
解方程得m=1或-4,
经检验m=1或-4均符合题意.
故答案为:1或-4;
(3)当m>1或m<-4时相交;
当-4<m<1时相离.
当m=3时,⊙M与直线AB的位置关系是相交;
(2)
 连接MN、MB、MC,则MN⊥AB,
连接MN、MB、MC,则MN⊥AB,在Rt△ABO中,AB2=OA2+OB2,AB=
| 62+32 |
| 5 |
在△AMB中,S△AMB=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=
| AM•OB |
| AB |
| (6-m)•3 | ||
3
|
| 6-m | ||
|
在Rt△OMC中,MC2=OM2+OC2,OM2=m2+4,
∵MN、MC均为⊙M的半径,
∴MN=MC,(
| 6-m | ||
|
解方程得m=1或-4,
经检验m=1或-4均符合题意.
故答案为:1或-4;
(3)当m>1或m<-4时相交;
当-4<m<1时相离.
点评:本题考查了直线与圆的位置关系、一元二次方程、三角形面积计算、勾股定理.做好本题的关键是根据题意理清思路,将几何问题转化为一元二次方程来求解.

练习册系列答案
相关题目
将抛物线y=2x2-4x-5向上平移6个单位长度,再向左平移2个单位长度,最后所得抛物线绕原点转180°,得到新的抛物线解析式( )
| A、y=2x2-4x-5 |
| B、y=-2x2+4x-1 |
| C、y=2x2+12x+19 |
| D、y=-2x2-12x-17 |
已知二次函数y=3x2-6x+5,若它的顶点不动,把开口反向,再沿对称轴平移,得到一条新抛物线,它恰好与直线y=mx-2交于点(2,4),则新抛物线的解析式为( )
| A、y=3x2+6x-4 |
| B、y=3x2+6x+4 |
| C、y=3x2-6x+4 |
| D、y=6x2-3x+4 |
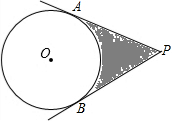 如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长. 如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?
如图,∠AOC=∠APQ=∠CFE=46°,可得到哪些平行线?为什么?