题目内容
如图，在Rt△ABC中，∠ABC=90°，DE垂直平分AC，垂足为点D，AB=3，EC=5，则BC的长为考点：线段垂直平分线的性质
专题：
分析：根据线段垂直平分线性质求出AE=EC=5，根据勾股定理求出BE，即可求出答案．
解答：
解：∵DE垂直平分AC，EC=5，
∴AE=EC=5，
∵在Rt△ABE中，∠C=90°，AB=3，AE=5，由勾股定理得：BE=4，
∴BC=BE+CE=4+5=9，
故答案为：9．
∴AE=EC=5，
∵在Rt△ABE中，∠C=90°，AB=3，AE=5，由勾股定理得：BE=4，
∴BC=BE+CE=4+5=9，
故答案为：9．
点评：本题考查了线段垂直平分线性质，勾股定理的应用，能求出BE长是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
顺次连结矩形四边中点所得的四边形一定是（ ）
| A、菱形 | B、矩形 |
| C、正方形 | D、等腰梯形 |
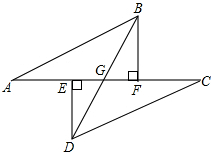如图，点A，E，F，C在同一条直线上，AE=CF，过点E，F分别作DE⊥AC，BF⊥AC，若AB=CD，求证：BD平分EF．
已知：如图，矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AB=4cm，求矩形对角线的长和矩形面积．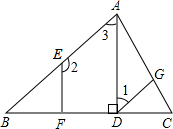
如图所示，已知AD⊥BC，垂足为点D，EF⊥BC，垂足为点F，∠1+∠2=180°．请填写∠CGD=∠CAB的理由．
如图，直线AB、CD相交于点O，若∠1+∠2=100°，则∠BOC等于（ ）| A、130° | B、140° |
| C、150° | D、160° |
如图，△ABC是等腰直角三角形，∠ABC=90°，D是AB延长线上一点，点E在BC边上，且BE=BD，连结AE，DC，∠BCD=15°，则∠AEC=
如图，△EDF中，∠EDF=90°，点B是EF的中点，点M在边ED上，过点B作MB的垂线交边DF于N点，求证：BM2+BN2=ME2+NF2．