题目内容
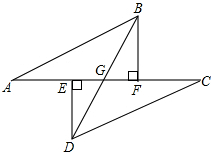 如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,若AB=CD,求证:BD平分EF.
如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,若AB=CD,求证:BD平分EF.考点:全等三角形的判定与性质
专题:证明题
分析:根据HL证出Rt△ABF≌Rt∠CDE,得出BF=DE,再根据AAS证出△BFG≌△DEG得出EG=FG,从而证得结论.
解答:
解:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°,
在Rt△ABF和Rt∠CDE中,
,
∴Rt△ABF≌Rt∠CDE(HL).
∴BF=DE,
在△BFG和△DEG中,
,
∴△BFG≌△DEG(AAS),
∴EG=FG,
即BD平分EF.
∴AE+EF=CF+EF,
∴AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°,
在Rt△ABF和Rt∠CDE中,
|
∴Rt△ABF≌Rt∠CDE(HL).
∴BF=DE,
在△BFG和△DEG中,
|
∴△BFG≌△DEG(AAS),
∴EG=FG,
即BD平分EF.
点评:本题考查了等边三角形的性质,三角形外角性质,全等三角形的性质和判定的应用,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
把(-2)2014+(-2)2015分解因式的结果是( )
| A、22015 |
| B、-22015 |
| C、-22014 |
| D、22014 |
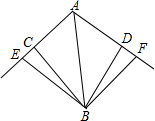 如图,BE和BF分别是两个钝角三角形ABC和ABD的高,BE=BF,BC=BD,求证:AC=AD.
如图,BE和BF分别是两个钝角三角形ABC和ABD的高,BE=BF,BC=BD,求证:AC=AD.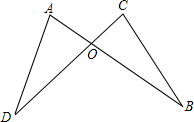 已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD.
已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD.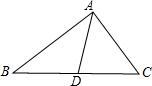 如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.
如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由. 如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长.
如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=7cm,AC=4cm,BC=6cm,求DE的长. 如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为
如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为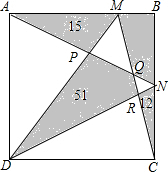 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为
如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为