题目内容
 如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.
如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.考点:全等三角形的判定与性质,勾股定理
专题:证明题
分析:延长NB到C,使BC=BN,连接CE、CM,根据SAS定理得出△BCE≌△BNF,故CE=NF,∠BEC=∠F.再由∠EDF=90°可知∠DEF+∠F=90°,故可得出∠CEM=90°,根据勾股定理可知ME2+CE2=CM2,即ME2+NF2=CM2.再由BM⊥BN得出BM2+BC2=CM2,即BM2+BN2=CM2进而可得出结论.
解答:
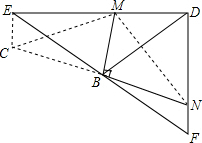 证明:延长NB到C,使BC=BN,连接CE、CM.
证明:延长NB到C,使BC=BN,连接CE、CM.
∵B是EF的中点,
∴BE=BF.
在△BCE与△BNF中,
∵
,
∴△BCE≌△BNF(SAS),
∴CE=NF,∠BEC=∠F.
∵∠EDF=90°,
∴∠DEF+∠F=90°,
∴∠DEF+∠BEC=90°即∠CEM=90°,
根据勾股定理
∴ME2+CE2=CM2,即ME2+NF2=CM2.
∵BM⊥BN,
∴BM2+BC2=CM2,即BM2+BN2=CM2
∴BM2+BN2=ME2+NF2.
 证明:延长NB到C,使BC=BN,连接CE、CM.
证明:延长NB到C,使BC=BN,连接CE、CM.∵B是EF的中点,
∴BE=BF.
在△BCE与△BNF中,
∵
|
∴△BCE≌△BNF(SAS),
∴CE=NF,∠BEC=∠F.
∵∠EDF=90°,
∴∠DEF+∠F=90°,
∴∠DEF+∠BEC=90°即∠CEM=90°,
根据勾股定理
∴ME2+CE2=CM2,即ME2+NF2=CM2.
∵BM⊥BN,
∴BM2+BC2=CM2,即BM2+BN2=CM2
∴BM2+BN2=ME2+NF2.
点评:本题考查的是全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
下列说法正确的是( )
| A、x+y是一次单项式 | ||||
B、多项式3
| ||||
| C、x的系数和次数都是1 | ||||
| D、单项式4×104x2的系数是4 |
 如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为
如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为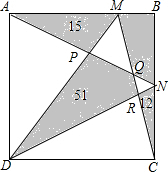 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为
如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为
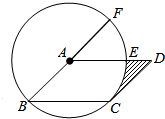 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F,已知