题目内容
顺次连结矩形四边中点所得的四边形一定是( )
| A、菱形 | B、矩形 |
| C、正方形 | D、等腰梯形 |
考点:中点四边形
专题:
分析:因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
解答:
 解:连接AC、BD,
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=
BD,
同理FG=
BD,HG=
AC,EF=
AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:A.
 解:连接AC、BD,
解:连接AC、BD,在△ABD中,
∵AH=HD,AE=EB
∴EH=
| 1 |
| 2 |
同理FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:A.
点评:本题考查了菱形的判定,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
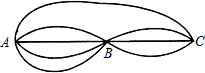 从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )
从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )| A、20种 | B、8种 | C、5种 | D、13 |
若|x-1|+(y-2)2+
=0,则x+y+z的值为( )
| z-3 |
| A、6 | B、5 | C、4 | D、3 |
把(-2)2014+(-2)2015分解因式的结果是( )
| A、22015 |
| B、-22015 |
| C、-22014 |
| D、22014 |
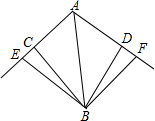 如图,BE和BF分别是两个钝角三角形ABC和ABD的高,BE=BF,BC=BD,求证:AC=AD.
如图,BE和BF分别是两个钝角三角形ABC和ABD的高,BE=BF,BC=BD,求证:AC=AD.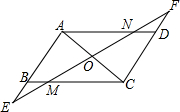 如图,已知:AB=DC,AD=BC.
如图,已知:AB=DC,AD=BC.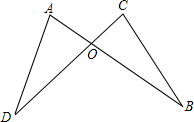 已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD.
已知,如图,AB,CD相交于点O,且AB=CD,AD=CB.试说明OB=OD. 如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为
如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为点D,AB=3,EC=5,则BC的长为