题目内容
从甲地到乙地是上坡路,从乙地到丙地是下坡路,王燕同学自甲地途径乙地到丙地,立即再沿原路返回甲地,共用3.5小时,已知王燕上坡速度相同,下坡速度也相同,并且走上坡路所用时间比下坡路所用时间多0.5小时.那么,王燕走上坡路共用了 小时.
考点:一元一次方程的应用
专题:行程问题,整体思想
分析:由于去时的上坡路即为回时的下坡路,去时的下坡路即为回时的上坡路.把王燕同学往返甲丙两地中的上坡路、下坡路分别看作一个整体,可设王燕走上坡路用了x小时,根据“走上坡路所用时间比下坡路所用时间多0.5小时”,可知她走下坡路用了(x-0.5)小时,由“王燕同学自甲地途径乙地到丙地,立即再沿原路返回甲地,共用3.5小时”得到等量关系:走上坡路所用时间+走下坡路所用时间=3.5小时,列出方程.
解答:解:设王燕走上坡路用了x小时,则她走下坡路用了(x-0.5)小时.
由题意,有x+(x-0.5)=3.5,
解得x=2.
即王燕走上坡路共用了2小时.
故答案为:2.
由题意,有x+(x-0.5)=3.5,
解得x=2.
即王燕走上坡路共用了2小时.
故答案为:2.
点评:本题考查了一元一次方程在行程问题中的应用.将王燕同学往返甲丙两地中的路程分为上坡路与下坡路,并把它们分别看作一个整体是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
一轮船从重庆到上海要6天,而从上海到重庆要8天,那么有一木排从重庆顺流漂到上海要( )
| A、24天 | B、38天 |
| C、48天 | D、49天 |
已知平面中有n个点A,B,C三个点在一条直线上,A,D,F,E四个点也在一条直线上,除些之外,再没有三点共线或四点共线,以这n个点作一条直线,那么一共可以画出38条不同的直线,这时n等于( )
| A、9 | B、10 | C、11 | D、12 |
设x1,x2是方程x2-2003x+2005=0的两个实根,实数a,b满足:ax12003+bx22003=2003,ax12004+bx22004=2004,则ax12005+bx22005的值为( )
| A、2005 | B、2003 |
| C、-2005 | D、-2003 |
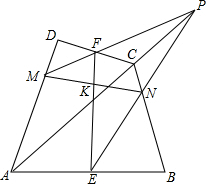 如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.
如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K. 如图△ABC中,∠B=45°,∠C=a(a>45°),AD是BC边上的高,E是AD上一点且DE=DC,延长BE交AC于F,∠ABF的大小是
如图△ABC中,∠B=45°,∠C=a(a>45°),AD是BC边上的高,E是AD上一点且DE=DC,延长BE交AC于F,∠ABF的大小是 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式