题目内容
 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式| (a+c)2 |
| (b-c)2 |
考点:二次函数图象与系数的关系,二次根式的性质与化简
专题:计算题
分析:根据二次函数的图象确定a,b,c的取值范围后再化简二次根式.
解答:解:由图知,二次函数y=ax2+bx+c的图象的开口向上,
∴a>0,
与y轴交于y轴的负半轴,c<0,
对称轴在一象限,-
>0,a>0,则b<0,
图象过点(-1,0),
因此a-b+c=0,a+c=b<0,b-c=a>0,
所以原式=-(a+c)+b-c=(-a+b)-2c=-a+b-2c.
故答案为:-a+b-2c.
∴a>0,
与y轴交于y轴的负半轴,c<0,
对称轴在一象限,-
| b |
| 2a |
图象过点(-1,0),
因此a-b+c=0,a+c=b<0,b-c=a>0,
所以原式=-(a+c)+b-c=(-a+b)-2c=-a+b-2c.
故答案为:-a+b-2c.
点评:本题利用了二次函数的图象确定a,b,c的取值范围后再化简二次根式,难度不大,注意二次根式的结果为非负数.

练习册系列答案
相关题目
 航导弹.
航导弹. 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,∠XOA=30°,则A、B两点的坐标分别是
如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,∠XOA=30°,则A、B两点的坐标分别是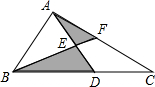 如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于
如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于