题目内容
已知平面中有n个点A,B,C三个点在一条直线上,A,D,F,E四个点也在一条直线上,除些之外,再没有三点共线或四点共线,以这n个点作一条直线,那么一共可以画出38条不同的直线,这时n等于( )
| A、9 | B、10 | C、11 | D、12 |
考点:一元二次方程的应用,相交线
专题:规律型
分析:解:假设n个点都不共线,则可画出直线
,若A,B,C三点不在一条直线上,可以画出3条直线,若A,D,E,F四点不在一条直线上,可以画出6条直线,所以有
-3-6+2,根据题意列方程求解即可.
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
解答:解:由n个点中每次选取两个点连直线,可以画出
条直线,若A,B,C三点不在一条直线上,可以画出3条直线,若A,D,E,F四点不在一条直线上,可以画出6条直线,
∴
-3-6+2=38.
整理得n2-n-90=0,(n-10)(n+90)=0.
∴n=10或n=-90(舍去0
故答案选B.
| n(n-1) |
| 2 |
∴
| n(n-1) |
| 2 |
整理得n2-n-90=0,(n-10)(n+90)=0.
∴n=10或n=-90(舍去0
故答案选B.
点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,本题的关键是先假设点都不在同一直线上,然后再把在同一直线上的情况去掉.

练习册系列答案
相关题目
在绝对值小于1000的整数中,完全平方数的个数是( )
| A、62 | B、63 | C、32 | D、31 |
 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,∠XOA=30°,则A、B两点的坐标分别是
如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,∠XOA=30°,则A、B两点的坐标分别是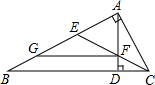 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠BCA的平分线交AD于F,交AB于E,FG∥BC交AB于G.AE=4,AB=14,则BG=
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠BCA的平分线交AD于F,交AB于E,FG∥BC交AB于G.AE=4,AB=14,则BG=