Question

某仓储系统有12条输入传送带，12条输出传送带．某日，控制室的电脑显示，每条输入传送带每小时进库的货物流量如图（1），每条输出传送带每小时出库的货物流量如图（2），而该日仓库中原有货物8吨，在0时至5时，仓库中货物存量变化情况如图（3）．

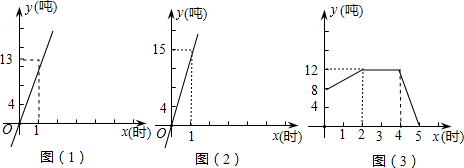
（1）每条输入传送带每小时进库的货物流量为多少吨？每条输出传送带每小时出库的货物流量为多少吨？
（2）在0时至5时内，仓库内货物存量y（吨）与时间x（小时）之间的函数关系式，并写出自变量x的取值范围；
（3）在4时至5时有多少条输入传送带和输出传送带在工作？

Answer 1

考点：一次函数的应用

专题：

分析：（1）根据图象，可得答案；
（2）根据待定系数法，可得函数解析式；
（3）根据二元一次方程，并根据x，y的取值范围（x≤20，y≤20，且都是正整数）可得出对应的答案．

解答：解：（1）由图象（1）得每条输入传送带每小时进库的货物流量为13吨，
由图象（2）得每条输出传送带每小时出库的货物流量为15吨；
（2）当0≤x＜2时，设函数解析式为y=kx+b，
函数y=kx+b图象过点（0，8）、（2，12），

2k+b=12 b=8

，解得

k=2 b=8

，
当0≤x＜2时，设函数解析式为y=2x+8，
当2≤x＜4时y=12，
当4≤x≤5时，设函数解析式为y=kx+b，
函数y=kx+b图象过点（4，12）、（5，0），

4k+b=12 5k+b=0

，解得

k=-12 b=60

，
当4≤x≤5时，设函数解析式为y=-12x+60；
仓库内货物存量y（吨）与时间x（小时）之间的函数关系式为y=

2x+8  (0≤x＜2) 12  (2≤x＜4) -12x+60  (4≤x≤5)

；
（3）设在4时至5时内有x条输入传送带和y条输出传送带在工作，则12+13x-15y=0，因为x≤20，y≤20，且都是正整数，所以x=6，y=6，
答：在4时至5时有6条输入传送带和6条输出传送带在工作．

点评：本题考查了一次函数的应用，解题关键是根据图象得出相关信息，根据题意列出方程，结合未知数的实际意义求解．