题目内容
设m是不小于-1的实数,使得关于x的方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1,x2.
(1)若
+
=1,求
的值;
(2)求
+
-m2的最大值.
(1)若
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| 3-2m |
(2)求
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
考点:根与系数的关系,根的判别式,二次函数的最值
专题:代数综合题
分析:(1)首先根据根的判别式求出m的取值范围,利用根与系数的关系,求出符合条件的m的值;
(2)把利用根与系数的关系得到的关系式代入代数式,细心化简,结合m的取值范围求出代数式的最大值.
(2)把利用根与系数的关系得到的关系式代入代数式,细心化简,结合m的取值范围求出代数式的最大值.
解答:解:∵方程有两个不相等的实数根,
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x1+x2=-2(m-2),x1x2=m2-3m+3,
∴
+
=
=
=1
解得:m1=
,m2=
(不合题意,舍去)
∴
=
-2.
(2)
+
-m2
=
-m2
=-2(m-1)-m2
=-(m+1)2+3.
当m=-1时,最大值为3.
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x1+x2=-2(m-2),x1x2=m2-3m+3,
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2(m-2) |
| m2-3m+3 |
解得:m1=
1-
| ||
| 2 |
1+
| ||
| 2 |
∴
| 1 |
| 3-2m |
| 5 |
(2)
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
=
| m(x1+x2)-2mx1x2 |
| 1-(x1+x2)+x1x2 |
=-2(m-1)-m2
=-(m+1)2+3.
当m=-1时,最大值为3.
点评:此题考查根与系数的关系,一元二次方程的根的判别式△=b2-4ac来求出m的取值范围;解答此题的关键是熟知一元二次方程根与系数的关系:x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
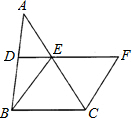 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.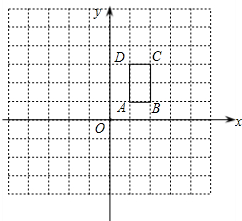 如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
 如图,在△ABC中,∠A=30°,∠B=50°,延长BC到D,则∠ACD=
如图,在△ABC中,∠A=30°,∠B=50°,延长BC到D,则∠ACD=