题目内容
(1)解不等式组
,并把解集在数轴上表示出来.
(2)因式分解:a2-8ab+16b2.
(3)解方程:
+
=
.
|
(2)因式分解:a2-8ab+16b2.
(3)解方程:
| 1 |
| x+2 |
| 4x |
| x2-4 |
| 2 |
| x-2 |
考点:解一元一次不等式组,因式分解-运用公式法,解分式方程,在数轴上表示不等式的解集
专题:
分析:(1)先求出每个不等式的解集,再求出不等式组的解集即可;
(2)根据完全平方公式分解即可;
(3)先化成整式方程,求出方程的解,最后进行检验即可.
(2)根据完全平方公式分解即可;
(3)先化成整式方程,求出方程的解,最后进行检验即可.
解答:解:(1)∵解不等式2x-5<0得:x<2.5,
解不等式x-2(x+1)<0得:x>-2,
∴不等式组的解集是-2<x<2.5,
在数轴上表示为: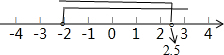 ;
;
(2)a2-8ab+16b2
=(a-4b)2;
(3)
+
=
,
方程两边都乘以(x+2)(x-2)得:
x-2+4x=2(x+2),
解得:x=2,
检验:∵当x=2时,(x+2)(x-2)=0,
∴x=2是方程的增根,
即原方程无解.
解不等式x-2(x+1)<0得:x>-2,
∴不等式组的解集是-2<x<2.5,
在数轴上表示为:
 ;
;(2)a2-8ab+16b2
=(a-4b)2;
(3)
| 1 |
| x+2 |
| 4x |
| x2-4 |
| 2 |
| x-2 |
方程两边都乘以(x+2)(x-2)得:
x-2+4x=2(x+2),
解得:x=2,
检验:∵当x=2时,(x+2)(x-2)=0,
∴x=2是方程的增根,
即原方程无解.
点评:本题考查了解一元一次不等式组,解分式方程,分解因式的应用,题目都比较典型,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,?ABCD的对角线AC和BD相交于点E,AC=24,BD=38,AD=28,则△ADE的周长是( )
如图,?ABCD的对角线AC和BD相交于点E,AC=24,BD=38,AD=28,则△ADE的周长是( )| A、59 | B、56 | C、51 | D、45 |

 如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为
如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为