Question

15．如图，在等腰梯形ABCD中，AD∥BC，E是BC上中点，DE∥AB，设$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{AB}$=$\overrightarrow{b}$，
（1）用含$\overrightarrow{a}$，$\overrightarrow{b}$的式子表示向量$\overrightarrow{DC}$；
（2）求作：$\overrightarrow{a}$-$\overrightarrow{b}$．（不写作法，保留作图痕迹，写出结果）

Answer 1

分析 （1）根据平行四边形的判定和性质得到$\overrightarrow{BE}$=$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{DE}$=$\overrightarrow{AB}$=$\overrightarrow{b}$，根据中点的定义得到$\overrightarrow{EC}$=$\overrightarrow{BE}$=$\overrightarrow{a}$，根据三角形法则即可求解；
（2）根据向量和差定义即可解决．

解答 解：（1）∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形，
∴$\overrightarrow{BE}$=$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{DE}$=$\overrightarrow{AB}$=$\overrightarrow{b}$，
∵E是BC上，
∴$\overrightarrow{EC}$=$\overrightarrow{BE}$=$\overrightarrow{a}$，
∴$\overrightarrow{DC}$=$\overrightarrow{DE}$+$\overrightarrow{EC}$=$\overrightarrow{b}$+$\overrightarrow{a}$；
（2）如图所示：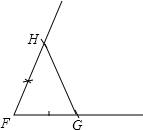

$\overrightarrow{GH}$就是所求的向量．

点评 本题考查梯形、平行四边形的性质，向量等知识，解题的关键是理解向量的定义以及向量和差定义，属于中考常考题型．