题目内容
阅读下面的文字,完成解答过程.
(1)如果有
=1-
=
-
=
-
,
则
= .
(2)用含有n的式子表示你发现的规律.
(3)根据(1)的规律来计算
+
+
+…+
的值.
(1)如果有
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
则
| 1 |
| 2013×2014 |
(2)用含有n的式子表示你发现的规律.
(3)根据(1)的规律来计算
| 1 |
| 1×4 |
| 1 |
| 4×7 |
| 1 |
| 7×10 |
| 1 |
| 2014×2017 |
考点:规律型:数字的变化类
专题:
分析:发现规律:(1)等式左边等于其分母上两因数的倒数之差;
(2)由(1)发现的规律用含有n的式子表示即可;
(3)首先计算每个分数的分母上两因数的倒数之差,再看其与该分数在数值上的区别,思考如何计算才能使二者相等.
(2)由(1)发现的规律用含有n的式子表示即可;
(3)首先计算每个分数的分母上两因数的倒数之差,再看其与该分数在数值上的区别,思考如何计算才能使二者相等.
解答:解:(1)
=
-
,
故答案为:
-
;
(2)
=
-
;
(3)
+
+
+…+
=
(1-
+
-
+
-
+…+
-
)
=
×(1-
)
=
×
=
.
| 1 |
| 2013×2014 |
| 1 |
| 2013 |
| 1 |
| 2014 |
故答案为:
| 1 |
| 2013 |
| 1 |
| 2014 |
(2)
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(3)
| 1 |
| 1×4 |
| 1 |
| 4×7 |
| 1 |
| 7×10 |
| 1 |
| 2014×2017 |
=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 10 |
| 1 |
| 2014 |
| 1 |
| 2017 |
=
| 1 |
| 3 |
| 1 |
| 2017 |
=
| 1 |
| 3 |
| 2016 |
| 2017 |
=
| 672 |
| 2017 |
点评:此题考查了数字变化类的规律型的题目,寻找与发现规律是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
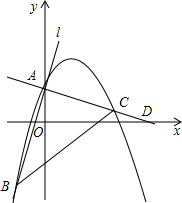 如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(-2,-4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D. 已知二次函数的图象(0≤x≤3)如图所示,关于函数在所给变量取值范围内,函数y最小值=
已知二次函数的图象(0≤x≤3)如图所示,关于函数在所给变量取值范围内,函数y最小值=
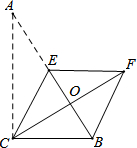 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是 如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),方程组
如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),方程组