题目内容
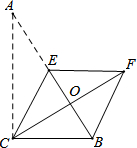 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;求出AC=3
,∠FCB=30°;此为解决该题的两个关键结论;证明四边形BCEF是平行四边形求出FM的长,即可解决问题.
| 3 |
解答: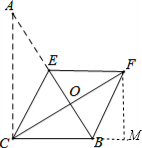 解:如图,过点F作FM⊥CB,交CB的延长线于点M;
解:如图,过点F作FM⊥CB,交CB的延长线于点M;
∵∠ACB=90°,∠A=30°,BC=3,
∴AB=6,AC=3
;AB=2BC;
∵点E是AB的中点,
∴AE=CE=BC,∠A=∠ACE=30°;
由翻折变换的性质得:
∠ECF=∠ECA=30°,∠A=∠EFC=30°,
AE=EF,CF=AC=3
;
∴∠FCB=90°-60°=30°,
∴∠EFC=∠FCB,
∴EF∥CB;而EF=BC,
∴四边形BCEF是平行四边形;
∵∠FCM=30°,CF=3
,FM⊥CM,
∴FM=
,
∴S平行四边形=BC•FM=3×
=
,
故答案为
.
 解:如图,过点F作FM⊥CB,交CB的延长线于点M;
解:如图,过点F作FM⊥CB,交CB的延长线于点M;∵∠ACB=90°,∠A=30°,BC=3,
∴AB=6,AC=3
| 3 |
∵点E是AB的中点,
∴AE=CE=BC,∠A=∠ACE=30°;
由翻折变换的性质得:
∠ECF=∠ECA=30°,∠A=∠EFC=30°,
AE=EF,CF=AC=3
| 3 |
∴∠FCB=90°-60°=30°,
∴∠EFC=∠FCB,
∴EF∥CB;而EF=BC,
∴四边形BCEF是平行四边形;
∵∠FCM=30°,CF=3
| 3 |
∴FM=
3
| ||
| 2 |
∴S平行四边形=BC•FM=3×
3
| ||
| 2 |
9
| ||
| 2 |
故答案为
9
| ||
| 2 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是作辅助线,灵活运用翻折变换的性质、直角三角形的性质来分析、判断、推理或解答.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
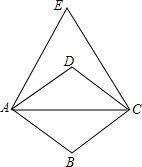 如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )
如图,四边形ABCD是菱形,以对角线AC为边向上作等边△ACE.已知∠DAB=70°,则∠EAD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |
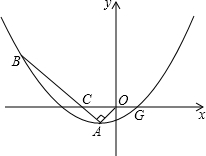 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴的一个交点为G(1,0).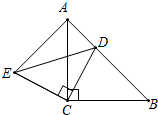 △ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.
△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.