题目内容
如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
(1)抛物线的解析式是 ;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′P=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.

(1)抛物线的解析式是
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′P=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.

考点:二次函数综合题
专题:
分析:(1)根据抛物线经过点C可求得c=3,再根据抛物线经过A,B点,即可求得a、b的值,即可解题;
(2)令PP′交DE于G,易证四边形FEPP′是平行四边形,可得PP′=EF,易证△DPP′∽△DAB,可得
=
,设EF=x,可得GE=4-x,即可求得y关于x的二次函数解析式,求得最大值即可解题;
(3)假设存在满足条件的点Q(x,y),作OH⊥BC于H,易证Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到,即可求得过Q点直线的解析式,即可解题.
(2)令PP′交DE于G,易证四边形FEPP′是平行四边形,可得PP′=EF,易证△DPP′∽△DAB,可得
| PP′ |
| AB |
| DE-GE |
| DE |
(3)假设存在满足条件的点Q(x,y),作OH⊥BC于H,易证Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到,即可求得过Q点直线的解析式,即可解题.
解答:解:(1)∵抛物线y=ax2+bx+c(a≠0)经过点C,
则c=3,
∵抛物线经过A,B两点,∴
解得:a=-1,b=2,
故答案为 y=-x2+2x+3;
(2)令PP′交DE于G,

∵PP′∥AF,PE∥FP′,
∴四边形FEPP′是平行四边形,
∴PP′=EF,
∴△DPP′∽△DAB,
∴
=
,
又∵A(-1,0)、B(3,0)、D(1,4),EF=x,
∴AB=4,DE=4,PP′=x,
∴
=
∴GE=4-x,
又∵S四边形EPP'F=EF•GE,
∴y=x(4-x)
∴y=x(4-x)=-(x-2)2+4,x=2时,y的最大值是4.
(3)假设存在满足条件的点Q(x,y),
作OH⊥BC于H,
∵Rt△BCQ中BC是直角边,
∴Rt△BCQ的另一直角边与OH平行.
又∵OC=OB,CO⊥OB,OB=3,OC=3,
∴Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到(如图).

由已知得直线OH的解析式是y=x,
∴Rt△BCQ的另一直角边所在的直线解析式是:y=x+3或 y=x-3
①点Q为直线y=x+3和抛物线交点,
则
,
解得:x=1,
∴y=4;
②点Q为直线y=x-3和抛物线交点,
则
,
解得:x=-2,
∴y=-5,
∴存在满足条件的点Q的坐标是:(1,4)和(-2,-5).
则c=3,
∵抛物线经过A,B两点,∴
|
解得:a=-1,b=2,
故答案为 y=-x2+2x+3;
(2)令PP′交DE于G,

∵PP′∥AF,PE∥FP′,
∴四边形FEPP′是平行四边形,
∴PP′=EF,
∴△DPP′∽△DAB,
∴
| PP′ |
| AB |
| DE-GE |
| DE |
又∵A(-1,0)、B(3,0)、D(1,4),EF=x,
∴AB=4,DE=4,PP′=x,
∴
| x |
| 4 |
| 4-GE |
| 4 |
∴GE=4-x,
又∵S四边形EPP'F=EF•GE,
∴y=x(4-x)
∴y=x(4-x)=-(x-2)2+4,x=2时,y的最大值是4.
(3)假设存在满足条件的点Q(x,y),
作OH⊥BC于H,
∵Rt△BCQ中BC是直角边,
∴Rt△BCQ的另一直角边与OH平行.
又∵OC=OB,CO⊥OB,OB=3,OC=3,
∴Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到(如图).

由已知得直线OH的解析式是y=x,
∴Rt△BCQ的另一直角边所在的直线解析式是:y=x+3或 y=x-3
①点Q为直线y=x+3和抛物线交点,
则
|
解得:x=1,
∴y=4;
②点Q为直线y=x-3和抛物线交点,
则
|
解得:x=-2,
∴y=-5,
∴存在满足条件的点Q的坐标是:(1,4)和(-2,-5).
点评:本题考查了抛物线解析式的求解,考查了二次函数最值的求解,考查了抛物线和直线交点的求解,本题中正确求得抛物线解析式是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
若式子
有意义,则x的取值范围为( )
| 1 | ||
4-
|
| A、x≥0 |
| B、x≠16 |
| C、x>0且x≠16 |
| D、x≥0且x≠16 |
正三角形的外接圆的半径为4,以正三角形的边长为边的正方形的外接圆的半径为( )
A、2
| ||
B、3
| ||
C、3
| ||
D、2
|
 一个舞台要铺地毯(如图中的阴影部分,扇形的圆心角为90°),若按每铺1m2地毯所需30元计算,共需多少元(损耗不计)?
一个舞台要铺地毯(如图中的阴影部分,扇形的圆心角为90°),若按每铺1m2地毯所需30元计算,共需多少元(损耗不计)?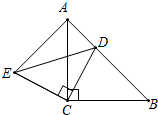 △ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.
△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.