题目内容
5.如图,在△ABC中,AB=BC=10,tan∠ABC=$\frac{4}{3}$,点P是边BC上的一点,在线段AP上取点M,将线段PM绕点P顺时针旋转90°得线段PN.设BP=t.(1)如图1,当点P在点B,点M是AP中点时,试求AN的长;
(2)如图2,当$\frac{PM}{MA}$=$\frac{1}{3}$时.
①求点N到BC边的距离(用含t的代数式表示);
②当点P从点B运动至点C时,试求点N运动路径的长.
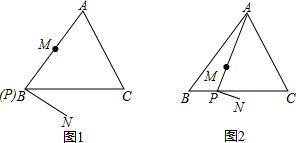
分析 (1)根据直角三角形中的勾股定理进行解答即可;
(2)①分0≤t≤6和6≤t≤10两种情况,利用相似三角形进行解答;
②利用勾股定理进行计算即可.
解答 解:(1)∵在Rt△ABC中,∠ABN=90°,AB=10,
∴BN=BM=$\frac{1}{2}$AB=5,
∴AN=$\sqrt{1{0}^{2}+{5}^{2}}=5\sqrt{5}$;
(2)①(Ⅰ)当0≤t≤6时(如图1)
过点A作AE⊥BC于点E,过点N作NF⊥BC于点F.
∵∠AEP=∠PFN=90°,∠APF+∠FPN=90°,∠APF+∠PAE=90°,
∴∠PAE=∠FPN,
∴△APE~△PNF,
∵$\frac{PM}{MA}$=$\frac{1}{3}$,
∴$\frac{PF}{AE}=\frac{FN}{PE}=\frac{PN}{AP}=\frac{1}{4}$,
∴DN=$\frac{1}{4}(6-t)=\frac{3}{2}-\frac{1}{4}t$;
(Ⅱ)当6≤t≤10时,
同理可得:DN=$\frac{1}{4}(t-6)=\frac{1}{4}t-\frac{3}{2}$;
②(如图2)点N的运动路径是一条线段,
当P与O重合时,$FN=\frac{3}{2}$,PF=2,
当P与C重合时,F′N′=1,PF′=2,
∴点N的路径长$N{N}^{'}=\sqrt{1{0}^{2}+(1+\frac{3}{2})^{2}}=\frac{5}{2}\sqrt{17}$.
点评 此题考查几何变换问题,关键是根据相似三角形的性质和勾股定理进行分析.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.关于一次函数y=2x-l的图象,下列说法正确的是( )
| A. | 图象经过第一、二、三象限 | B. | 图象经过第一、三、四象限 | ||
| C. | 图象经过第一、二、四象限 | D. | 图象经过第二、三、四象限 |
13. 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )| A. | 6 | B. | 12 | C. | 32 | D. | 64 |
20.现有点数为2,3,4,5的四张扑克牌,背面朝上洗匀,然后从中任意抽取从中任意抽取两张,这两张牌上的数字之和为偶数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
10. 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
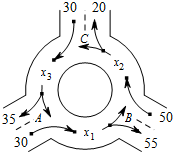 如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)
如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)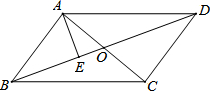 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.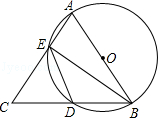 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.