题目内容
10. 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
分析 根据已知条件⊙O的直径CD⊥AB,可知$\widehat{AC}$=$\widehat{BC}$,所以它们所对的圆周角相等,然后利用圆周角定理来求∠AOC的大小.
解答 解:∵⊙O的直径CD⊥AB,
∴AE=BE,
∴$\widehat{AC}$=$\widehat{BC}$,
∴$\widehat{AC}$与$\widehat{BC}$所对的圆周角∠CDB相等;
∴∠CDB=$\frac{1}{2}$∠AOC;
∵∠CDB=25°,
∴∠AOC=50°.
故选D.
点评 本题考查了圆周角定理和垂径定理.解答此题的关键是理清弧的关系,找出等弧,则可根据等弧所对的圆周角相等.

练习册系列答案
相关题目
2. 如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
 如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )| A. | 30° | B. | 60° | C. | 120° | D. | 180° |
20. 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
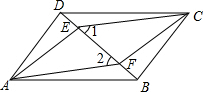 如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2. 如图,AB∥CD,E是CD上的一点,BE,CF交于点F.若∠B=45°,∠C=60°,则∠BFC=105°.
如图,AB∥CD,E是CD上的一点,BE,CF交于点F.若∠B=45°,∠C=60°,则∠BFC=105°.