题目内容
14.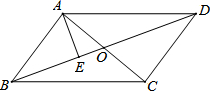 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.(1)用尺规作CF⊥BD于点F(要求保留作图痕迹,不要求写作法与证明);
(2)求证:AE=CF.
分析 (1)以C为圆心,大于AE长为半径画弧,分别交BD于点M,N两点,再分别以M,N为圆心,以大于$\frac{1}{2}$MN为半径画弧,交于点G,连接CG并延长,交BD于点F,即可得CF⊥BD于点F;
(2)由AE⊥BD于点E,CF⊥BD于点F,可得∠AEO=∠CFO=90°,又由在平行四边形ABCD中,OA=OC,即可利用AAS,判定△AOE≌△COF,继而证得结论.
解答  解:(1)如图,①以C为圆心,大于AE长为半径画弧,分别交BD于点M,N两点,
解:(1)如图,①以C为圆心,大于AE长为半径画弧,分别交BD于点M,N两点,
②再分别以M,N为圆心,以大于$\frac{1}{2}$MN为半径画弧,交于点G,
③连接CG并延长,交BD于点F,
即CF为所求;
(2)∵在平行四边形ABCD中,OA=OC,
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEO=∠CFO=90°,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS),
∴AE=CF.
点评 本题主要考查较简单的尺规作图,平行四边形的性质,全等三角形的判定与性质.注意证得△AOE≌△COF是关键.

练习册系列答案
相关题目
2. 如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
 如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )| A. | 30° | B. | 60° | C. | 120° | D. | 180° |
9.某中学九年级(1)班体检结果出来后,一位同学对全班同学的身高(单位:厘米)统计如下表:
这组数据的众数为( )
| 身高(厘米) | 159 | 160 | 162 | 165 | 167 | 168 |
| 人数 | 3 | 5 | 8 | 18 | 10 | 8 |
| A. | 159 | B. | 162 | C. | 165 | D. | 167 |
 将自然数0,1,2,3…做如下数表的排列,则2015排在第45行,从左向右数的第36个数.
将自然数0,1,2,3…做如下数表的排列,则2015排在第45行,从左向右数的第36个数.
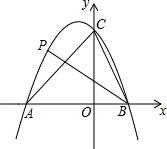 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6). 如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.