题目内容
15.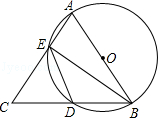 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.(1)求证:△CDE∽△CAB;
(2)求证:DE=BD;
(2)如果BC=6,AB=5,求BE的长.
分析 (1)由圆内接四边形的性质得出∠CED=∠CBA,再由公共角相等,即可证出△CDE∽△CAB;
(2)由等腰三角形的性质得出∠C=∠CBA,证出∠C=∠CED,得出DE=CD,再由圆周角定理和三线合一性质得出CD=BD,即可得出DE=BD;
(3)由割线定理求出CE,由圆周角定理得出∠AEB=∠BEC=90°,根据勾股定理即可求出BE的长.
解答 (1)证明:连接AD,如图所示: ∵四边形ABDE是⊙O的内接四边形,
∵四边形ABDE是⊙O的内接四边形,
∴∠CED=∠CBA,
又∵∠C=∠C,
∴△CDE∽△CAB;
(2)证明:∵AB=AC,
∴∠C=∠CBA,
∴∠C=∠CED,
∴DE=CD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴CD=BD,
∴DE=BD;
(3)解:由割线定理得:CE•AC=CD•BC,
∵CD=BD=$\frac{1}{2}$BC=3,AC=AB=5,
∴CE=$\frac{CD•BC}{AC}$=$\frac{3×6}{5}$=$\frac{18}{5}$,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠BEC=90°,
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{{6}^{2}-(\frac{18}{5})^{2}}$=$\frac{24}{5}$.
点评 本题考查了圆内接四边形的性质、相似三角形的判定、等腰三角形的性质、圆周角定理、割线定理、勾股定理;本题有一定难度,特别是(2)(3)中,需要运用圆周角定理、割线定理和勾股定理才能得出结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
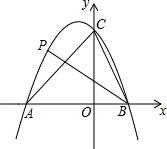 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6). 在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.
在△ABC中,∠C=90°,AB=10,点D在AB边上,且CD=BD,则CD的长为5.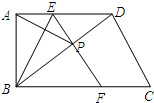 如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c. 如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.
如图,在?ABCD中,E,F分别为AB,CD的中点,求证:GH=$\frac{1}{2}$DC.