题目内容
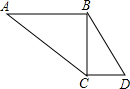
 如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.
如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.考点:勾股定理
专题:
分析:连接AC,先根据AB⊥BC,AB=5,BC=12求出AC的长,再判断出△ACD的形状,根据三角形的面积公式即可得出结论.
解答: 解:连接AC,过点C作CE⊥AD于点E,
解:连接AC,过点C作CE⊥AD于点E,
∵AB⊥BC,AB=5,BC=12,
∴AC=
=
=13,
∵CD=13,
∴AC=CD=13,
∵AD=10,
∴AE=
AD=5,
∴CE=
=
=12.
∴S四边形ABCD=S△ABC+S△ACD=
AB•BC+
AD•CE=
×5×12+
×10×12=30+60=90.
 解:连接AC,过点C作CE⊥AD于点E,
解:连接AC,过点C作CE⊥AD于点E,∵AB⊥BC,AB=5,BC=12,
∴AC=
| AB2+BC2 |
| 52+122 |
∵CD=13,
∴AC=CD=13,
∵AD=10,
∴AE=
| 1 |
| 2 |
∴CE=
| AC2-AE2 |
| 132-52 |
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 如图,∠ABC=∠BCD=90°,AB=8,sinA=
如图,∠ABC=∠BCD=90°,AB=8,sinA= 到姜堰观光旅游的客人越来越多,某景点每天都吸引大量的游客前来观光.事实表明,如果游客过多,不利于保护珍贵文物,为了实施可持续发展,兼顾社会效益和经济效益,该景点拟采用浮动门票价格的方法来控制游览人数.已知每张门票原价为40元,现设浮动门票为每张x元,且40<x<70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
到姜堰观光旅游的客人越来越多,某景点每天都吸引大量的游客前来观光.事实表明,如果游客过多,不利于保护珍贵文物,为了实施可持续发展,兼顾社会效益和经济效益,该景点拟采用浮动门票价格的方法来控制游览人数.已知每张门票原价为40元,现设浮动门票为每张x元,且40<x<70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.