题目内容
15.体积V(dm3)一定的长方体,则它的底面积y(dm2)与高x(m)之间的函数图象大致为( )| A. | 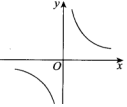 | B. | 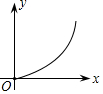 | C. | 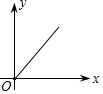 | D. | 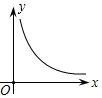 |
分析 由题意y=$\frac{v}{x}$,(x>0),v是定值,所以y是x的反比例函数,由此即可解决问题.
解答 解:由题意y=$\frac{v}{x}$,(x>0),v是定值,
∴y是x的反比例函数,图象在第一象限,
故选D.
点评 本题考查反比例函数的性质,解题的关键是理解反比例函数的定义,灵活运用所学知识解决问题.

练习册系列答案
相关题目
3.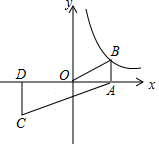 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的解析式;
(2)求△ACD的面积.
 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.(1)求这个反比函数的解析式;
(2)求△ACD的面积.
20.我市2013年平均房价为每平方米13000元,连续两年增长后,2015年平均房价达到每平方米15500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 15500(1+x)2=13000 | B. | 15500(1-x)2=13000 | C. | 13000(1+x)2=15500 | D. | 13000(1-x)2=15500 |
7. 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
 如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )
如图,矩形ACBD中,AB=5,BC=12,AB的中垂线与BC交于点E,与AD交于F,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
4.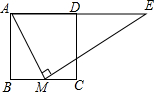 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )| A. | 18 | B. | $\frac{109}{5}$ | C. | $\frac{96}{5}$ | D. | $\frac{25}{3}$ |
5.有这样一个问题:探究函数y=x-1+$\frac{1}{x-2}$的图象与性质.
下面是小东的探究过程,请补充完成:
(1)函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2.
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
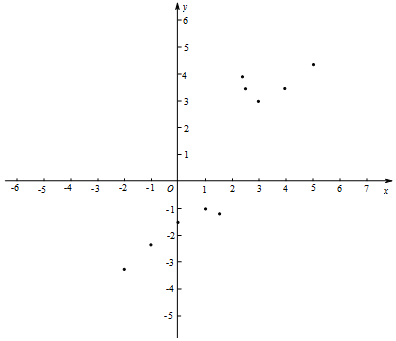
(3)求m的值;
(4)根据图象写出此函数的一条性质.
下面是小东的探究过程,请补充完成:
(1)函数y=x-1+$\frac{1}{x-2}$的自变量x的取值范围是x≠2.
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
| y | … | -3.25 | -2.33 | -1.50 | -1 | -1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |

(3)求m的值;
(4)根据图象写出此函数的一条性质.
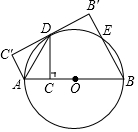 如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.