题目内容
4.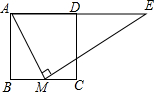 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )| A. | 18 | B. | $\frac{109}{5}$ | C. | $\frac{96}{5}$ | D. | $\frac{25}{3}$ |
分析 先根据题意得出△ABM∽△MCG,故可得出CG的长,再求出DG的长,根据△MCG∽△EDG即可得出结论.
解答  解:∵四边形ABCD是正方形,AB=12,BM=5,
解:∵四边形ABCD是正方形,AB=12,BM=5,
∴MC=12-5=7.
∵ME⊥AM,
∴∠AME=90°,
∴∠AMB+∠CMG=90°.
∵∠AMB+∠BAM=90°,
∴∠BAM=∠CMG,∠B=∠C=90°,
∴△ABM∽△MCG,
∴$\frac{AB}{MC}$=$\frac{BM}{CG}$,即$\frac{12}{7}$=$\frac{5}{CG}$,解得CG=$\frac{35}{12}$,
∴DG=12-$\frac{35}{12}$=$\frac{109}{12}$.
∵AE∥BC,
∴∠E=CMG,∠EDG=∠C,
∴△MCG∽△EDG,
∴$\frac{MC}{DE}$=$\frac{CG}{DG}$,即$\frac{7}{DE}$=$\frac{\frac{35}{12}}{\frac{109}{12}}$,解得DE=$\frac{109}{5}$.
故选B.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
9.用计算器计算时,下列说法错误的是( )
| A. | 计算“$\frac{1}{2}$-1$\frac{3}{4}$”的按键顺序是 | |
| B. | 计算“3×105-28”的按键顺序是 | |
| C. | “已知SinA=0.3,求锐角A”的按键顺序是 | |
| D. | 计算“($\frac{1}{2}$)5”的按键顺序是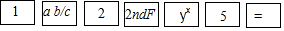 |
16.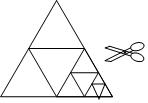 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( )| A. | 332 | B. | 333 | C. | 334 | D. | 335 |
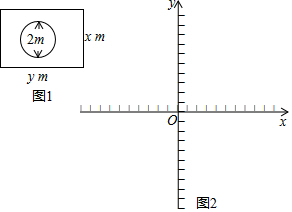 2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.
2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.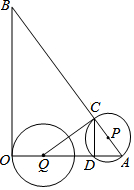 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.