题目内容
从放有3个白球和2个红球的袋子中,每次任取一球,记下颜色后再放回去,这样连续取两次.
(1)试计算第一次取到白球且第二次取到红球的概率为多少?
(2)若取出的球不放回,求两次取到的球都是红球的概率.
(1)试计算第一次取到白球且第二次取到红球的概率为多少?
(2)若取出的球不放回,求两次取到的球都是红球的概率.
考点:列表法与树状图法
专题:
分析:(1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两次都摸到白球的情况,再利用概率公式求解即可求得答案;
(2)利用树状图法即可求解.
(2)利用树状图法即可求解.
解答:解:(1)列表得:
∵共有25种等可能的结果,两次都摸到红球的有9种情况,
∴两次都摸到白球的概率是:
.
(2)

共有20种等可能的结果,两次都摸到红球的有6种情况,则两次都摸到红球的概率是:
=
.
| 红白 | 红白 | 红白 | 白白 | 白白 |
| 红白 | 红白 | 红白 | 白白 | 白白 |
| 红红 | 红红 | 红红 | 白红 | 白红 |
| 红红 | 红红 | 红红 | 白红 | 白红 |
| 红红 | 红红 | 红红 | 白红 | 白红 |
∴两次都摸到白球的概率是:
| 9 |
| 25 |
(2)

共有20种等可能的结果,两次都摸到红球的有6种情况,则两次都摸到红球的概率是:
| 6 |
| 20 |
| 3 |
| 10 |
点评:此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
已知命题A:“关于x的一元二次方程x2-2ax+1=0一定有实根”.在下列选项中,可以作为“命题A是假命题”的反例的是( )
| A、a=-3 | B、a=-1 |
| C、a=0 | D、a=2 |
在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在所给的下列条件中能判断△ABC不是直角三角形的是( )
| A、∠A=∠C-∠B | ||||
| B、a2=c2-b2 | ||||
C、a=k,b=
| ||||
| D、a:b:c=2:3:4 |
 小彬的爸爸制作了一件边框为长方形的工艺品,挂在墙上很漂亮,但小彬看来看去总觉得它不像长方形,经过思考小彬仅用一把刻度尺(尺的长度足够)就解决了问题,你能说出他用的是什么方法吗?(简要说明一下操作过程及相关理由)
小彬的爸爸制作了一件边框为长方形的工艺品,挂在墙上很漂亮,但小彬看来看去总觉得它不像长方形,经过思考小彬仅用一把刻度尺(尺的长度足够)就解决了问题,你能说出他用的是什么方法吗?(简要说明一下操作过程及相关理由)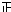
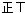
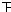
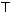
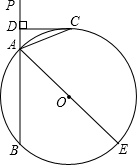 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.