题目内容
在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在所给的下列条件中能判断△ABC不是直角三角形的是( )
| A、∠A=∠C-∠B | ||||
| B、a2=c2-b2 | ||||
C、a=k,b=
| ||||
| D、a:b:c=2:3:4 |
考点:勾股定理的逆定理,三角形内角和定理
专题:
分析:利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解答:解:A、由条件可得∠A+∠B=∠C,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC为直角三角形;
B、由条件可得a2+b2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;
C、由条件有a2+b2=k2+(
k)2=3k2=(
k)2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、设a=2x,则b=3x,c=4x,由a2+b2=(2x)2+(3x)2=13x2≠(4x)2=c2,不满足勾股定理的逆定理,故△ABC不是直角三角形;
故选D.
B、由条件可得a2+b2=c2,满足勾股定理的逆定理,故△ABC是直角三角形;
C、由条件有a2+b2=k2+(
| 2 |
| 3 |
D、设a=2x,则b=3x,c=4x,由a2+b2=(2x)2+(3x)2=13x2≠(4x)2=c2,不满足勾股定理的逆定理,故△ABC不是直角三角形;
故选D.
点评:本题主要考查直角三角形的判定方法,掌握判定直角三角形的方法是解题的关键,可以利用定义也可以利用勾股定理的逆定理.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
下列事件中,是必然事件的是( )
| A、掷一枚均匀的正方形骰子,骰子停止后朝上的点数是2 |
| B、篮球队员在罚球线上投篮一次,未投中 |
| C、买1张彩票一定会中奖 |
| D、四边形的内角和360° |
若
=
,则
=( )
| m+n |
| m-n |
| 7 |
| 3 |
| m |
| m-n |
A、
| ||
B、
| ||
C、
| ||
D、
|
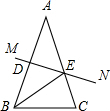 如图,在△ABC中,AC=12,边AB的垂直平分线分别交AB、AC于点D、E,若BC=8,则△BCE的周长为( )
如图,在△ABC中,AC=12,边AB的垂直平分线分别交AB、AC于点D、E,若BC=8,则△BCE的周长为( )| A、20 | B、22 | C、24 | D、26 |
