题目内容
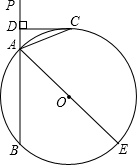 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;
(2)若CD=4,⊙O的直径为10,求BD的长度.
考点:切线的判定
专题:
分析:(1)连接OC,根据题意可证得∠CAD+∠DCA=90°,再根据角平分线的性质,得∠DCO=90°,则CD为⊙O的切线;
(2)过O作OF⊥AB,则∠OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形,在Rt△AOF中,由勾股定理得AF2+OF2=OA2,从而求得AF的值,进而就可求得BD的长.
(2)过O作OF⊥AB,则∠OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形,在Rt△AOF中,由勾股定理得AF2+OF2=OA2,从而求得AF的值,进而就可求得BD的长.
解答: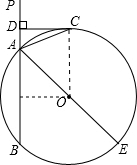 (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴CD⊥OC,CO为⊙O半径,
∴CD为⊙O的切线;
(2)解:过O作OF⊥AB,垂足为F,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD=5,OF=CD=4.
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
∴AF=
=
=3,
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴FB=AF=3.
∴BD=DF+BF=5+3=8.
 (1)证明:连接OC,
(1)证明:连接OC,∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴CD⊥OC,CO为⊙O半径,
∴CD为⊙O的切线;
(2)解:过O作OF⊥AB,垂足为F,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD=5,OF=CD=4.
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
∴AF=
| OA2-OF2 |
| 52-42 |
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴FB=AF=3.
∴BD=DF+BF=5+3=8.
点评:本题考查了切线的判定和性质、勾股定理、矩形的判定和性质以及垂径定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
若-
=a,则a满足( )
| 7 |
| A、-4<a<-3 |
| B、-3<a<-2 |
| C、-2<a<-1 |
| D、-1<a<0 |
下列事件中,是必然事件的是( )
| A、掷一枚均匀的正方形骰子,骰子停止后朝上的点数是2 |
| B、篮球队员在罚球线上投篮一次,未投中 |
| C、买1张彩票一定会中奖 |
| D、四边形的内角和360° |
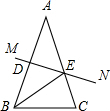 如图,在△ABC中,AC=12,边AB的垂直平分线分别交AB、AC于点D、E,若BC=8,则△BCE的周长为( )
如图,在△ABC中,AC=12,边AB的垂直平分线分别交AB、AC于点D、E,若BC=8,则△BCE的周长为( )| A、20 | B、22 | C、24 | D、26 |
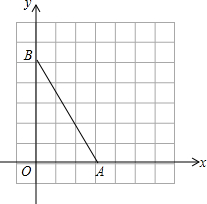 平面直角坐标系中,已知O为坐标原点,点A(3,0),B(0,3
平面直角坐标系中,已知O为坐标原点,点A(3,0),B(0,3
 如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,CD=11,BC=2,求对角线AC的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,CD=11,BC=2,求对角线AC的长. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是
如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是