题目内容
14.下列四组线段中,可以构成直角三角形的是( )| A. | 4,5,6 | B. | 1,$\sqrt{2}$,3 | C. | 2,3,4 | D. | 1.5,2,2.5 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、42+52≠62,不能构成直角三角形,故不符合题意;
B、12+($\sqrt{2}$)2≠32,不能构成直角三角形,故不符合题意;
C、32+22=42,不能构成直角三角形,故不符合题意;
D、1.52+22=2.52,能构成直角三角形,故符合题意.
故选:D.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B的坐标为( )| A. | (6,6) | B. | (6,8) | C. | (8,6) | D. | (8,2) |
6.若4x2-kx+49是完全平方式,则k的值为( )
| A. | 28 | B. | -28 | C. | ±28 | D. | ±196 |
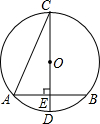 如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为3$\sqrt{2}$cm.
如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为3$\sqrt{2}$cm.