题目内容
3．用适当的方法解下列方程（1）（x+3）2=5（x+3）
（2）2x2-x+3=0．
分析 （1）方程整理后，利用因式分解法求出解即可；
（2）方程利用公式法求出解即可．
解答 解：（1）方程移项得：（x+3）2-5（x+3）=0，
分解因式得：（x+3）（x+3-5）=0，
解得：x1=-3，x2=2；
（2）2x2-x+3=0，
∵a=2，b=-1，c=3，
∴b2-4ac=1-24=-23＜0，
则此方程无解．
点评 此题考查了解一元二次方程-因式分解法，以及公式法，熟练掌握各种解法是解本题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
14．下列四组线段中，可以构成直角三角形的是（ ）
| A． | 4，5，6 | B． | 1，$\sqrt{2}$，3 | C． | 2，3，4 | D． | 1.5，2，2.5 |
11．下列判断中正确的是（ ）
| A． | 3a2bc与3ab2c是同类项 | B． | $\frac{{{m^2}+1}}{5}$是单项式 | ||
| C． | 单项式-x3y2的系数是-1 | D． | 3x2-y+5xy2是二次三项式 |
18．使式子$\sqrt{-{x}^{2}}$有意义的x是（ ）
| A． | 全体正数 | B． | 全体负数 | C． | 零 | D． | 非零数 |
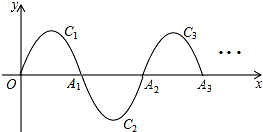一段抛物线y=-x（x-3），（0≤x＞3），记为C1，它与x轴交于点O，A1，将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C672．若P（2015，m）在图象上，则m=-2．
15．解下列分式方程
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
13．已知a＜0，那么点（3-a，-a2-3）关于y轴的对称点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |