题目内容
2.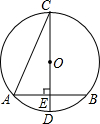 如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为3$\sqrt{2}$cm.
如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为3$\sqrt{2}$cm.
分析 连结OA,如图,由OA=OC得到∠OCA=∠CAO=22.5°,则利用三角形外角性质可得∠AOD=45°,接着根据垂径定理得到AE=BE,且可判断△OAE为等腰直角三角形,然后根据等腰直角三角形的性质可得AE=$\frac{\sqrt{2}}{2}$OA=$\frac{3\sqrt{2}}{2}$,所以AB=2AE=3$\sqrt{2}$cm.
解答 解:连结OA,如图,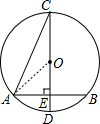
∵OA=OC,
∴∠OCA=∠CAO=22.5°,
∴∠AOD=45°,
∵CD⊥AB,
∴AE=BE,△OAE为等腰直角三角形,
而CD=6,
∴OA=3,
∴AE=$\frac{\sqrt{2}}{2}$OA=$\frac{3\sqrt{2}}{2}$,
∴AB=2AE=3$\sqrt{2}$(cm).
故答案为3$\sqrt{2}$.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的性质.

练习册系列答案
相关题目
17.已知⊙O的半径为5cm,直线L上有一点P到圆心距离等于5,则直线L与⊙O的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相交或相切 |
14.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,$\sqrt{2}$,3 | C. | 2,3,4 | D. | 1.5,2,2.5 |
11.下列判断中正确的是( )
| A. | 3a2bc与3ab2c是同类项 | B. | $\frac{{{m^2}+1}}{5}$是单项式 | ||
| C. | 单项式-x3y2的系数是-1 | D. | 3x2-y+5xy2是二次三项式 |
