题目内容
8. 已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:
已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:(1)这个二次函数的解析式;
(2)△ABP的面积.
分析 (1)根据待定系数法求得即可;
(2)根据求得的解析式化成顶点式,求得顶点P的坐标,然后根据待定系数法求得直线BP的解析式,求得与y轴的交点坐标,然后根据S△PAB=S△AMB+S△PAM求得即可.
解答  解:(1)把点A和点B分别代入y=x2+bx+c,得$\left\{\begin{array}{l}{c=-2}\\{1+b+c=1}\end{array}\right.$,
解:(1)把点A和点B分别代入y=x2+bx+c,得$\left\{\begin{array}{l}{c=-2}\\{1+b+c=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=-2}\end{array}\right.$
∴二次函数的解析式为:y=x2+2x-2;
(2)由y=x2+2x-2=(x+1)2-3可知:顶点P(-1,-3)
设直线BP的解析式为y=mx+n,
把B(1,1),P(-1,-3)代入得$\left\{\begin{array}{l}{m+n=1}\\{-m+n=-3}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$
∴直线BP的解析式为y=2x-1,
当x=0时,y=-1,
∴M(0,-1),
∵A(0,-2)
∴AM=1,
∴△ABP的面积=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1=1.
点评 本题考查了待定系数法求二次函数的解析式和一次函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3.下列命题不是真命题的是( )
| A. | 等腰梯形对角线相等 | |
| B. | 一组对边平行另一组对边相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
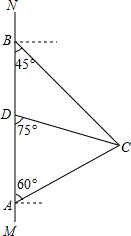 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.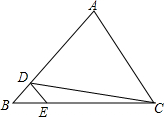 如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )