题目内容
18.不等式组$\left\{\begin{array}{l}{x-1>2x}\\{3x-2>2(x-2)}\end{array}\right.$的解集为-2<x<-1.分析 先求出每个不等式的解集,再求出公共部分即可.
解答 解:$\left\{\begin{array}{l}{x-1>2x①}\\{3x-2>2(x-2)②}\end{array}\right.$
解不等式①得:x<-1,
解不等式②得:x>-2,
∴不等式组的解集为-2<x<-1,
故答案为:-2<x<-1.
点评 本题考查了解一元一次不等式组的应用,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
6.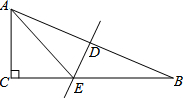 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )| A. | 15 | B. | 15$\sqrt{2}$ | C. | 30 | D. | 30$\sqrt{2}$ |
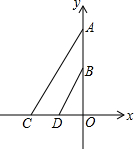 如图,平面直角坐标系中,A(0,10),B(0,5),点C是x轴上一点,点D为OC的中点.
如图,平面直角坐标系中,A(0,10),B(0,5),点C是x轴上一点,点D为OC的中点.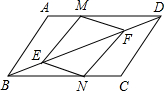 如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.
如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.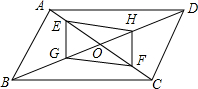 如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE.
如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE. 尺规作图,保留作图痕迹,不写作法.
尺规作图,保留作图痕迹,不写作法.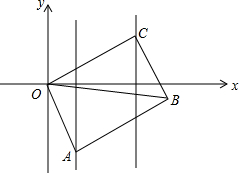 如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.
如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.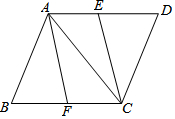 如图,在?ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
如图,在?ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.