题目内容
7. 如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.
如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.
分析 过点B作BD⊥直线x=5,交直线x=5于点D,过点B作BE⊥x轴,交x轴于点E.则由勾股定理可求出OB的长.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
解答 解: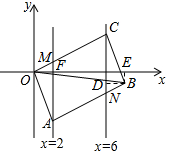 过点B作BD⊥直线x=5,交直线x=5于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,直线x=5与AB交于点N,如图:
过点B作BD⊥直线x=5,交直线x=5于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,直线x=5与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=5均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
$\left\{\begin{array}{l}{∠FOA=∠DBC}\\{OA=BC}\\{∠OAF=∠BCD}\end{array}\right.$,
∴△OAF≌△BCD(ASA).
∴BD=OF=2,
∴OE=5+2=7,
∴OB=$\sqrt{O{E}^{2}+B{E}^{2}}$.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=7.
故答案为:7.
点评 本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,如果汽车第一次右拐60°那么第二次拐弯应该( )
| A. | 左拐60° | B. | 右拐60° | C. | 左拐120° | D. | 右拐120° |
16.多项式m2-m与多项式2m2-4m+2的公因式是( )
| A. | m-1 | B. | m+1 | C. | m2-1 | D. | (m-1)2 |
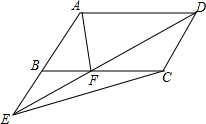 如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.
如图,E是?ABCD中AB延长线上一点,ED交BC于点F,求证:S△ABF=S△CEF.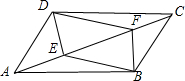 已知:如图,四边形DEBF是平行四边形,且AE=CF.
已知:如图,四边形DEBF是平行四边形,且AE=CF.