题目内容
3.甲、乙、丙、丁四名射击运动员分别连续射靶10次,他们各自的平均成绩及其方差如表所示,如果选一名成绩好且发挥稳定的运动员参赛,则应选择的运动员是丙.| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩(环) | 8.6 | 8.4 | 8.6 | 7.6 |
| 方差 | 0.94 | 0.74 | 0.56 | 1.92 |
分析 首先比较平均数,平均数相同时选择方差较小的运动员参加即可.
解答 解:∵$\overline{{x}_{甲}}$=$\overline{{x}_{丙}}$>$\overline{{x}_{乙}}$=$\overline{{x}_{丁}}$,
∴从甲和丙中选择一人参加比赛,
∵S甲2><S丙2,
∴选择丙参赛,
故答案为:丙.
点评 本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
相关题目
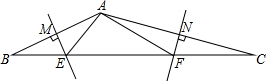
 如图,平行四边形ABCD的对角线AC,BD相交于点0,E、F分别是0A、0C的中点,求证:△DOF≌△BOE.
如图,平行四边形ABCD的对角线AC,BD相交于点0,E、F分别是0A、0C的中点,求证:△DOF≌△BOE.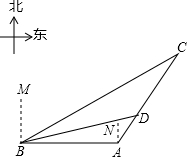 今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75$\sqrt{2}$海里.
今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75$\sqrt{2}$海里.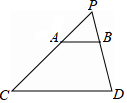 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.