题目内容
2.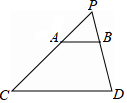 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB离地面的距离为1.8m.
分析 直接利用相似三角形的判定与性质得出两三角形的相似比,再利用对应高的比也等于相似比进而得出答案.
解答 解:∵AB∥CD,
∴△PAB∽△PCD,
∵AB=2m,CD=6m,
∴$\frac{AB}{CD}$=$\frac{1}{3}$,
∵点P到CD的距离是2.7m,设AB离地面的距离为:xm,
∴$\frac{2.7-x}{2.7}$=$\frac{1}{3}$,
解得:x=1.8,
故答案为:1.8.
点评 此题主要考查了相似三角形的应用,正确利用相似三角形的性质分析是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
2. 如图,将一副三角板叠合在一起(∠AOB=∠COD=90°,∠A=30°,∠C=45°),使直角顶点重合,AB与OC交于点E,若∠AOD=3∠BOC,则∠OEA的度数为( )
如图,将一副三角板叠合在一起(∠AOB=∠COD=90°,∠A=30°,∠C=45°),使直角顶点重合,AB与OC交于点E,若∠AOD=3∠BOC,则∠OEA的度数为( )
 如图,将一副三角板叠合在一起(∠AOB=∠COD=90°,∠A=30°,∠C=45°),使直角顶点重合,AB与OC交于点E,若∠AOD=3∠BOC,则∠OEA的度数为( )
如图,将一副三角板叠合在一起(∠AOB=∠COD=90°,∠A=30°,∠C=45°),使直角顶点重合,AB与OC交于点E,若∠AOD=3∠BOC,则∠OEA的度数为( )| A. | 95° | B. | 105° | C. | 115° | D. | 120° |
3.甲、乙、丙、丁四名射击运动员分别连续射靶10次,他们各自的平均成绩及其方差如表所示,如果选一名成绩好且发挥稳定的运动员参赛,则应选择的运动员是丙.
| 甲 | 乙 | 丙 | 丁 | |
| 平均成绩(环) | 8.6 | 8.4 | 8.6 | 7.6 |
| 方差 | 0.94 | 0.74 | 0.56 | 1.92 |
 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=$\sqrt{3}$,则图中阴影部分的面积为$\frac{\sqrt{3}}{2}$.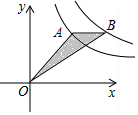 如图,在直角坐标系中,点A是反比例函数y=$\frac{2}{x}$图象在第一象限上的一点,过点A作x轴的平行线交反比例函数y=$\frac{4}{x}$图象于点B,当点A的横坐标逐渐增大时,则△ABO的面积变化情况是( )
如图,在直角坐标系中,点A是反比例函数y=$\frac{2}{x}$图象在第一象限上的一点,过点A作x轴的平行线交反比例函数y=$\frac{4}{x}$图象于点B,当点A的横坐标逐渐增大时,则△ABO的面积变化情况是( )