题目内容
 已知CD∥AE,∠1=∠2,∠3=∠4,判断△ABC是否是直角三角形,说明理由.
已知CD∥AE,∠1=∠2,∠3=∠4,判断△ABC是否是直角三角形,说明理由.考点:平行线的性质
专题:
分析:根据平行线的性质,两直线平行,同旁内角互补,以及∠1=∠2,∠3=∠4,即可证得∠2+∠3=90°,根据三角形内角和定理即可证得∠ABC=90°,从而求解.
解答:解:∵CD∥AE,
∴∠DCA+∠CAE=180°,
又∵∠1=∠2,∠3=∠4,即∠2=
∠DCA,∠3=
∠CAE,
∴∠2+∠3=
(∠DCA+∠CAE)=90°,
∴∠ABC=180°-(∠2+∠3)=90°,
∴△ABC是直角三角形.
∴∠DCA+∠CAE=180°,
又∵∠1=∠2,∠3=∠4,即∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2+∠3=
| 1 |
| 2 |
∴∠ABC=180°-(∠2+∠3)=90°,
∴△ABC是直角三角形.
点评:本题比较简单,考查的是平行线的性质:两直线平行,同旁内角互补.及三角形内角内角和定理.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结DE.若AB=8,CD=2,则DE的长为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结DE.若AB=8,CD=2,则DE的长为( )A、4
| ||
B、5
| ||
C、4
| ||
D、3
|
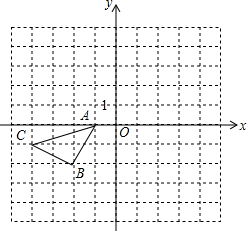 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: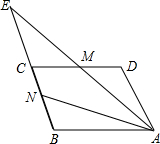 如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设
如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设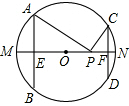 如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN 于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值为
如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN 于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值为