题目内容
 如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.
如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.(1)若∠AOB=56°,求∠ADC的度数;
(2)若BC=6,AE=1,求⊙O的半径.
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)利用圆周角与圆心角的关系即可求解.
(2)利用垂径定理可以得到CE=BE=
BC=3,然后根据勾股定理即可求得.
(2)利用垂径定理可以得到CE=BE=
| 1 |
| 2 |
解答:解:(1)∵OA⊥BC,
∴
=
,
∴∠ADC=
∠AOB,
∵∠AOB=56°,
∴∠ADC=28°;
(2)∵OA⊥BC,
∴CE=BE,
设⊙O的半径为r,则OE=r-1,OB=r
在Rt△BOE中,OE2+BE2=OB2,
∵BE=3,则32+(r-1)2=r2
解得这个方程,得r=5.
∴
 |
| AC |
 |
| AB |
∴∠ADC=
| 1 |
| 2 |
∵∠AOB=56°,
∴∠ADC=28°;
(2)∵OA⊥BC,
∴CE=BE,
设⊙O的半径为r,则OE=r-1,OB=r
在Rt△BOE中,OE2+BE2=OB2,
∵BE=3,则32+(r-1)2=r2
解得这个方程,得r=5.
点评:此题考查了圆周角与圆心角定理以及垂径定理,熟练掌握垂径定理是解题关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,已知点A、F、C、D在同一条直线上,AC=DF,BC∥EF,只需补充一个条件,就可得△ABC≌△DEF.则下列条件中不符合要求的是( )
如图,已知点A、F、C、D在同一条直线上,AC=DF,BC∥EF,只需补充一个条件,就可得△ABC≌△DEF.则下列条件中不符合要求的是( )| A、AB=DE |
| B、BC=EF |
| C、∠B=∠E |
| D、AB∥DE |
 如图,函数y=-﹙x-1﹚2+c的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )
如图,函数y=-﹙x-1﹚2+c的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )| A、-4 | B、-3 | C、-2 | D、-1 |

 如图,已知反比例函数y1=
如图,已知反比例函数y1=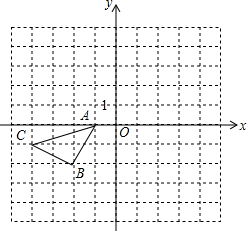 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: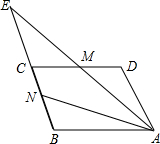 如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设
如图,已知M、N分别是平行四边形ABCD边DC、BC的中点,射线AM和射线BC相交于E,设