题目内容
3.如果三角形的两边长分别是方程x2-10x+24=0的两个根,那么连接该三角形三边中点所得的三角形的周长可能是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 先利用因式分解法解方程得到x1=4,x2=6,则利用三角形三边的关系得到三角形的第三边长在2与10之间,所以三角形的周长在12与20之间,然后根据三角形中位线性质得到连接该三角形三边中点所得的三角形的周长在6与10之间,再利用此结论对各选项进行判断.
解答 解:x2-10x+24=0
(x-4)(x-6)=0,
x-4=0或x-6=0,
x1=4,x2=6,
所以三角形的第三边长在2与10之间,
所以三角形的周长在12与20之间,
所以连接该三角形三边中点所得的三角形的周长在6与10之间.
故选B.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了三角形三边的关系和三角形中位线性质.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
14.下列方程是关于x的一元二次方程的是( )
| A. | (x+1)2=x+1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0 | C. | $\sqrt{{x}^{2}-1}$=0 | D. | x2+2x=x2-1 |
18.如果(x2-mx-n)(x-3)的乘积中不含x2项和x项,那么( )
| A. | m=0,n=0 | B. | m=-3,n=-9 | C. | m=-3,n=9 | D. | m=3,n=-9 |
15.设ab≠0,a2+b2=1,如果x=$\frac{{a}^{4}+{b}^{4}}{{a}^{6}+{b}^{6}}$,y=$\frac{{a}^{4}+{b}^{4}}{\sqrt{{a}^{4}+{b}^{4}}}$,z=$\frac{\sqrt{{a}^{4}+{b}^{4}}}{{a}^{6}+{b}^{6}}$,那么x,y,z的大小关系是( )
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | y<x<z |
7. 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
 如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )| A. | AE=CD | B. | AE>CD | C. | AE<CD | D. | 无法确定 |
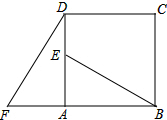 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.
如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7.