题目内容
14.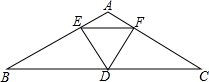 如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
分析 由∠A=120°,AB=AC,易得∠B=∠C=30°,从而得∠EDF=60°,因为D是BC的中点,易证△BDE≌△CDF,由全等三角形的性质得DE=DF,由等边三角形的判定得△DEF是等边三角形.
解答 证明:∵∠A=120°,AB=AC,
∴∠B=∠C=30°,
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∴∠BDE=∠CDF=60°,
∴∠EDF=60°,
∵D是BC的中点,
∴BD=CD,
在△BDE与△CDF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CD}\\{∠BDE=∠CDF}\end{array}\right.$,
∴△BDE≌△CDF,
∴DE=DF,
∴△DEF是等边三角形.
点评 本题主要考查了等腰三角形的性质,全等三角形的性质及判定定理,等边三角形的判定,找出等边三角形的判定条件是解答此题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
16.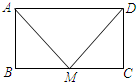 如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
 如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )| A. | ∠AMD=90° | B. | AM是∠BAD的平分线 | ||
| C. | AM:AD=1:$\sqrt{2}$ | D. | AB:BC=1:$\sqrt{2}$ |
 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1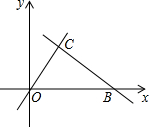 如图,直线OC、BC的函数关系式为y=x与y=-2x+6,点P(t,0)是线段OB上一动点,过P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式为y=x与y=-2x+6,点P(t,0)是线段OB上一动点,过P作直线l与x轴垂直.