题目内容
15．已知CD是Rt△ABC的斜边AB上的高，AD、BD是x2-6x+4=0的两根，求△ABC的面积．分析 由AD、BD是方程x2-6x+4=0的两根可以得到AD+BD=6，AD•BD=4，易证△DBC∽△DCA，可得到CD=$\sqrt{AD•BD}$=2，而△ABC的面积=$\frac{1}{2}$×（AD+BD）×CD，由此可以求出面积．
解答 解：∵AD、BD是方程x2-6x+4=0的两根，
∴AD+BD=6，AD•BD=4，
∵∠ACB=90°，CD⊥AB于D，
∴△DBC∽△DCA，
∴$\frac{CD}{AD}=\frac{DB}{CD}$，
∴CD2=AD•BD，
∴CD=$\sqrt{AD•BD}$=2，
∴S△ABC=$\frac{1}{2}$×（AD+BD）×CD=6．
点评 本题考查了相似三角形的判定和性质，勾股定理，此题难点是利用相似求得斜边上的高，解题关键是得到所求三角形相应的底与高的长．
练习册系列答案
相关题目
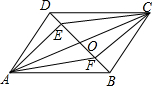在?ABCD中，对角线AC、BD相交于点O，点E、F在对角线BD上，且OE=OF．
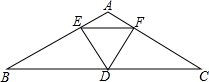如图，在△ABC中，∠A=120°，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，点E，F为垂足，求证：△DEF是等边三角形．
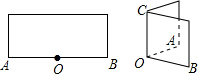将一张长方形对折，使OA与OB重合，这时∠AOC是什么角？为什么？
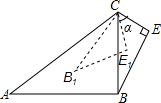如图，在△ABC和△BCE中，∠CBE=30°，∠BEC=90°，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B1，E的对应点为E1，设直线B1E1与直线BE交于点F，与直线CB交于点Q，当△BPQ为等腰三角形时，α的大小是30°，75°或165°．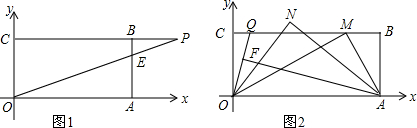
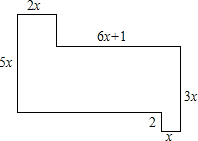如图的面积为22x2+4x （以x来表示）
如图，点P是矩形ABCD的边AD上一动点，矩形的两条 边长AB、BC分别为8和15，则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$．