题目内容
5.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+y=5k}\\{x-y=9k}\end{array}\right.$的解也是二元一次方程2x+3y=6的解,则k-$\frac{1}{2}$的算术平方根为$\frac{1}{2}$.分析 先用含k的代数式表示x、y,即解关于x,y的方程组,再代入2x+3y=-6中可得k的值,最后根据算术平方根求解即可.
解答 解:方程组$\left\{\begin{array}{l}{x+y=5k}\\{x-y=9k}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=7k}\\{y=-2k}\end{array}\right.$,
把x,y代入二元一次方程2x+3y=6,
得:2×7k+3×(-2k)=6,
解得:k=$\frac{3}{4}$,
则k-$\frac{1}{2}$=$\frac{3}{4}-\frac{1}{2}=\frac{1}{4}$,
$\frac{1}{4}$的算术平方根为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 此题考查的知识点是二元一次方程组的解,先用含k的代数式表示x,y,即解关于x,y的方程组,再代入2x+3y=6中可得.其实质是解三元一次方程组.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
16.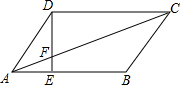 如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
 如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )
如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD为( )| A. | 3 | B. | 27 | C. | 6 | D. | 12 |
13. 如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )
如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )
 如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )
如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )| A. | 16分40秒 | B. | 30分 | C. | 15分 | D. | 14分40秒 |
20.在同一个圆中,四条半径将圆分割成扇形A,B,C,D的面积之比为2:3:3:4,则最大扇形的圆心角为( )
| A. | 80° | B. | 100° | C. | 120° | D. | 150° |
14.解方程4(2x+5)2=5(5+2x)最合适的方法是( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法 | D. | 因式分解法 |
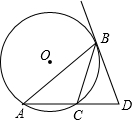 如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径为1,∠D=60°,求CD的长.
如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径为1,∠D=60°,求CD的长. 已知如图所示,⊙O1与⊙O2外切于点T,过点T作直线分别交⊙O1,⊙O2于A、B两点,⊙O1,⊙O2的半径分别是2和3,求AT:BT的值.
已知如图所示,⊙O1与⊙O2外切于点T,过点T作直线分别交⊙O1,⊙O2于A、B两点,⊙O1,⊙O2的半径分别是2和3,求AT:BT的值.