题目内容
6. 如图,点A、B、C在⊙O上,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连结CD.
如图,点A、B、C在⊙O上,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连结CD.(1)求证:CD与⊙O相切;
(2)若CD=6,求图中阴影部分(弓形BC劣弧所对)的面积.(结果保留π和根号)
分析 (1)利用圆周角定理进而得出∠COB=∠AOB-∠AOC=60°,进而得出△COB是等边三角形,再利用等腰三角形的性质得出∠OCD=90°,即可得出答案;
(2)直接利用S阴影=S扇形OBC-S△OBC,进而得出答案.
解答 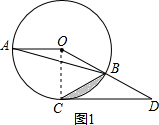 (1)证明:如图1,连接OC,
(1)证明:如图1,连接OC,
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
又∵∠AOB=150°,
∴∠COB=∠AOB-∠AOC=60°,
∵OC=OB,
∴△COB是等边三角形,
∴BC=OB,∠OBC=∠OCB=60°,
∵BD=OB,
∴BC=BD,
∴∠BCD=∠D=$\frac{1}{2}$∠OBC=30°,
∴∠OCD=90°,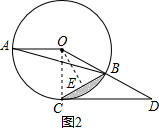
∴CD与⊙O相切;
(2)解:如图2,作OE⊥BC于点E,
在Rt△OCD中
∵tan∠D=$\frac{OC}{CD}$=$\frac{\sqrt{3}}{3}$,
∴OC=2$\sqrt{3}$,
在Rt△OCE中,OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=3,
S阴影=S扇形OBC-S△OBC,
=$\frac{60π×O{C}^{2}}{360}$-$\frac{1}{2}$×BC•EO,
=2π-3$\sqrt{3}$.
点评 此题主要考查了切线的判定以及等边三角形的性质与判定、勾股定理、扇形面积求法等知识,正确得出扇形OBC的面积是解题关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
16. 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
请根据图表信息解答下列问题:
(1)a=35;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
(1)a=35;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?

 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时