题目内容
10.解答下列各题:(1)解不等式6(x-1)≥3+4x
(2)解不等式$\frac{x-2}{2}$<$\frac{7-x}{3}$
(3)解不等式$\frac{x-5}{2}$+1>x-3,请把它的解集表示在数轴上
(4)解不等式组$\left\{\begin{array}{l}{3(x+1)>5x-1}\\{\frac{5x+1}{2}-\frac{2x-1}{3}≥-1}\end{array}\right.$,并求出它的整数解.
分析 (1)去括号,移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可;
(3)去分母,去括号,移项,合并同类项,系数化成1即可;
(4)先求出不等式组的解集,再求出整数解即可.
解答 解:(1)6(x-1)≥3+4x,
6x-6≥3+4x,
6x-4x≥3+6,
2x≥9,
x≥4.5;
(2)$\frac{x-2}{2}$<$\frac{7-x}{3}$,
3(x-2)<2(7-x),
3x-6<14-2x,
3x+2x<14+6,
5x<20,
x<4;
(3)$\frac{x-5}{2}$+1>x-3,
x-5+2>2x-6,
x-2x>-6+5-2,
-x>-3,
x<3,
在数轴上表示为: ;
;
(4)$\left\{\begin{array}{l}{3(x+1)>5x-1①}\\{\frac{5x+1}{2}-\frac{2x-1}{3}≥-1②}\end{array}\right.$
∵解不等式①得:x<2,
解不等式②得:x≥-1,
∴不等式组的解集为-1≤x<2,
∴不等式组的整数解为-1,0,1.
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式的解集,不等式组的整数解等知识点,能求出不等式组或不等式的解集是解此题的关键.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
20.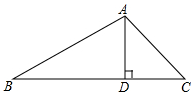 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
18.已知不等式组$\left\{\begin{array}{l}{x≥-a-1}\\{-x≥-b}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,求b-a的值.


19.某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价),这两种服装的进价、标价如表所示:
求这两种服装各购进的件数.
| 价格类型 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
 如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.
如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.

 如图,直线AC∥BD,BC平分∠ABD,DE⊥BC,∠MAB=80°,求∠EDB的度数.
如图,直线AC∥BD,BC平分∠ABD,DE⊥BC,∠MAB=80°,求∠EDB的度数.