题目内容
2.如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD,BC相交于点M,N,
(1)那么∠1与∠2有什么关系?请说明理由;
(2)若将过O点的直线旋转至图(2)(3)的情况下,其他条件不变,那么(1)中的关系还成立吗?请说明理由.
分析 (1)如图(1),证明AM∥CN,得到△AMO∽△CNO;进而得到∠1=∠2,$\frac{AM}{CN}$=$\frac{AO}{CO}$,结合AO=CO,即可解决问题.
(2)如图(2),运用与(1)中,类似的方法,证明证明AM∥CN,得到△AMO∽△CNO;进而得到∠1=∠2,$\frac{AM}{CN}$=$\frac{AO}{CO}$,结合AO=CO,即可解决问题.
解答 解;(1)∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AM∥CN,△AMO∽△CNO
∴∠1=∠2;$\frac{AM}{CN}$=$\frac{AO}{CO}$,
∵AO=CO,
∴AM=CN.
(2)在图(2)、(3)两种情况下,
(1)中的结论仍然成立.
以图(2)说明如下:∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AD∥BC,△AMO∽△CNO
∴∠1=∠2;$\frac{AM}{CN}$=$\frac{AO}{CO}$,
∵AO=CO,
∴AM=CN;
以图(3)说明如下:∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AD∥BC,△AMO∽△CNO
∴∠1=∠2;$\frac{AM}{CN}$=$\frac{AO}{CO}$,
∵AO=CO,
∴AM=CN.
点评 该题主要考查了旋转的性质,平行四边形的判定等几何知识点及其应用问题;解题的关键是牢固掌握定理本质内容,灵活运用动态的观念,来观察、分析、运动图形中的不变元素.

练习册系列答案
相关题目
 如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)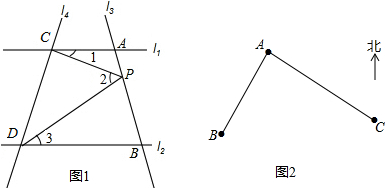
 如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.
如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.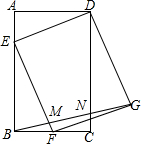 如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.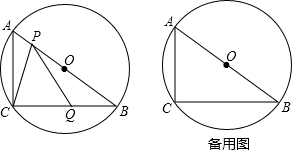
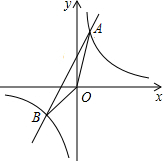 已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(1,8),B(-4,m),
已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(1,8),B(-4,m),