题目内容
5．
已知二次函数y=2x2-4x-6．（1）写出对称轴和顶点坐标；
（2）在平面直角坐标系中，画出这个二次函数的图象；
（3）当x取何值时，y＜0．
分析 （1）把函数一般式转化为顶点坐标式，进而写出对称轴和顶点坐标；
（2）利用描点法画二次函数图象；
（3）根据函数图象，写出函数图象在x轴下方所对应的自变量的取值范围即可．
解答 解：（1）y=2x2-4x-6=2（x-1）2-8，则抛物线的对称轴为直线x=1，顶点坐标为（1，-8），
（2）当y=0时，2x2-4x-6=0，解得x1=-1，x2=3．
所以抛物线与x轴的两交点坐标为（-1，0），（3，0）；
当x=0时，y=2x2-4x-6=-6，则抛物线与y轴的交点坐标为（0，-6）；
如图，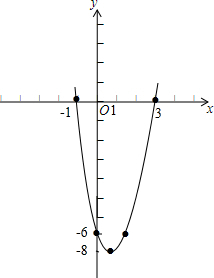
（3）当-1＜x＜3时，y＜0．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数图象．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
已知：如图，在正方形ABCD外取一点E，连接AE，BE，DE．过点A作AE的垂线AP交DE于点P．若AE=AP=1，PB=$\sqrt{6}$，下列结论：
20．方程$\frac{1}{x+2}$+$\frac{1}{x-2}$=$\frac{4}{{{x^2}-2}}$（ ）
| A． | x=2 | B． | x=-2 | C． | 无解 | D． | 以上都不对 |
在矩形AOBC中，OB=4，OA=3，分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系xOy，F是边BC上的一个动点（不与B，C重合），过点F的反比例函数y=$\frac{k}{x}$（k＞0）的图象与边AC交于点E，连接OE，OF．
甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑摩托车，甲到达B地停留半小时后返回A地．如图是他们离A地的距离y（千米）与时间x（小时）之间的函数关系图象．