题目内容
7.直角三角形的两条直角边长分别为16和12,则此三角形的外接圆半径是10,内切圆半径是4.分析 首先根据勾股定理求得该直角三角形的斜边是10,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解答 解:由勾股定理可知:当两条直角边长分别为16和12,则直角三角形的斜边长=$\sqrt{1{6}^{2}+1{2}^{2}}$=20.
根据直角三角形的外接圆的半径是斜边的一半,则其外接圆的半径是10;
根据直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半,则其内切圆的半径是4.
故答案为10,4.
点评 此题要熟记直角三角形外接圆的半径和内切圆的半径公式:外接圆的半径等于斜边的一半;内切圆的半径等于两条直角边的和与斜边的差的一半.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
17.如果x个人y天做了a个零件,那么y个人用相同的速度做x个零件需要的天数是( )
| A. | $\frac{{x}^{2}}{a}$ | B. | $\frac{a}{{x}^{2}}$ | C. | $\frac{{a}^{2}}{x}$ | D. | $\frac{x}{{a}^{2}}$ |
16.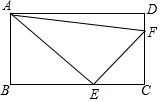 如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
 如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )
如图,在矩形ABCD中,AB=2,BC=3,AE是∠BAD的平分线,EF⊥AE,则AF的长为( )| A. | 3$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | $\sqrt{10}$ |
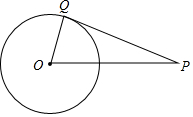 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6.