题目内容
17.如图,在平面直角坐标系中,直线y=x+n与抛物线y=ax2+bx+3相交子点A(-5,-7)、B(5,c),点C、D在直线AB上,且点D在点C的右侧,过点C、D分别作CF、DE平行于y轴交抛物线于点F、E,以点C、D、E、F为顶点的多边形记作图形M,其面积为S,设点C的横坐标为m,点D的横坐标为m+2,当-5<m<5时,解答下列问题:(1)求直线与抛物线所对应的函数关系式;
(2)求s与m的函数关系式;
(3)当M为中心对称图形时,求m的值;
(4)将M沿直线AB翻折,E、F两点的对应点为E′、F′,请直接写出C、D、E、F四个点中有且只有两个点同时落在第四象限时m的取值范围.
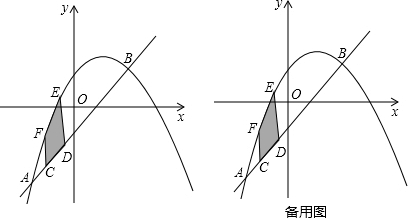
分析 (1)由直线y=x+n经过点A(-5,-7),B(5,c),求出n,c,把A(-5,-7),B(5,3)代入y=ax2+bx+3解方程组即可.
(2)分两种情形讨论:求出FC、ED,根据梯形的面积公式计算即可.
(3)分两种情形讨论:当M为平行四边形时,M为中心对称图形,由CF=DE,列出方程计算即可.
(4)分别求出当点F′落在y轴上时(如图1中),m的值;当点D在y轴上时(如图2中),m的值;当点D在x轴上时(如图3中),m的值;当点C在x轴上时(如图4中),m的值,由此即可解决问题.
解答 解:(1)∵直线y=x+n经过点A(-5,-7),B(5,c),
∴-7=-5+n,
∴n=-2.
∴c=5-2=3,
∴直线解析式为y=x-2.
把A(-5,-7),B(5,3)代入y=ax2+bx+3得到$\left\{\begin{array}{l}{25a-5b+3=-7}\\{25a+5b+3=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\frac{1}{5}}\\{b=1}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{5}$x2+x+3.
(2)①当-5<m≤3时,
∵点C横坐标为m,
∴C(m,m-2),D(m+2,m),F(m,-$\frac{1}{5}$m2+m+3),E[m+2,-$\frac{1}{5}$(m+2)2+(m+2)+3],
∴FC=-$\frac{1}{5}$m2+m+3-(m-2)=-$\frac{1}{5}$m2+5,ED=-$\frac{1}{5}$(m+2)2+5,
∴S=$\frac{1}{2}$×2×[-$\frac{1}{5}$m2+5-$\frac{1}{5}$(m+2)2+5]
=-$\frac{2}{5}$m2-$\frac{2}{5}$m+$\frac{46}{5}$.
②当3<m<5时,S=S=$\frac{1}{2}$×2×[-$\frac{1}{5}$m2+5+$\frac{1}{5}$(m+2)2-5]=$\frac{4}{5}$m+$\frac{4}{5}$
(3)①当-5<m≤3时,当M为平行四边形时,M为中心对称图形,
∴CF=DE,
∴-$\frac{1}{5}$m2+5=-$\frac{1}{5}$(m+2)2+5,
解得m=-1.
②当3<m<5时,可得-$\frac{1}{5}$m2+5=$\frac{1}{5}$(m+2)2-5,
解得m=-1+2$\sqrt{6}$或-1-2$\sqrt{6}$(舍弃),
综上所述,m=-1或-1+2$\sqrt{6}$.
(4)如图1中,当点F′落在y轴上时,因为C(m,m-2),则F(m,-$\frac{1}{5}$m2+m+3),
∵CF=CF′,
∴-m=-$\frac{1}{5}$m2+m+3-(m-2),
解得:m=$\frac{5-5\sqrt{5}}{2}$或$\frac{5+5\sqrt{2}}{2}$(舍弃),
如图2中,当点D在y轴上时,m+2=0,m=-2,
如图3中,当点D在x轴上时,m+2=2,m=0,
如图4中,当点C在x轴上时,m=2,
综上所述,当C、D、E′、F′四个点中有且只有两个点同时落在第四象限时m的取值范围为$\frac{5-5\sqrt{5}}{2}$<m≤-2,或0<m<2.
点评 本题考查二次函数的综合题、翻折变换、一次函数.梯形的面积公式等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会分类讨论,学会可以特殊位置考虑问题,找到问题的突破口,属于中考压轴题.

 期末集结号系列答案
期末集结号系列答案 如图,已知△ABC,用直尺和圆规求作一直线AD,使直线过顶点A,且平分△ABC的面积(不需写作法,保留作图痕迹)
如图,已知△ABC,用直尺和圆规求作一直线AD,使直线过顶点A,且平分△ABC的面积(不需写作法,保留作图痕迹)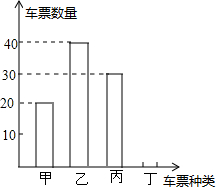 “五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题: