题目内容
7.抛物线y=x2+2x-1与坐标轴的交点个数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 先根据△的意义判断抛物线与x轴有交点个数,然后加上抛物线与y轴的交点为(0,-1),从而可判断抛物线y=x2+2x-1与坐标轴的交点个数.
解答 解:∵△=22-4×1×(-1)=8>0,
∴抛物线与x轴有两个交点,
∵抛物线与y轴的交点坐标为(0,-1),
∴抛物线y=x2+2x-1与坐标轴的交点个数为3个.
故选A.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数(△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点).

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,已知AB为⊙O的直径,点D为半圆周上一点,且$\widehat{AD}$=2$\widehat{BD}$,则∠BOD=120°,∠AOD=60°.
如图,已知AB为⊙O的直径,点D为半圆周上一点,且$\widehat{AD}$=2$\widehat{BD}$,则∠BOD=120°,∠AOD=60°.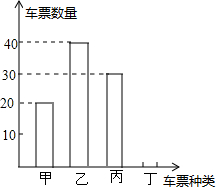 “五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题: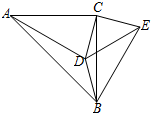 如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是( )
如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是( )