题目内容
1．若关于x的一元二次方程x2+2x-3=0的两根为x1，x2，则2x1+2x2+x1x2=-1．分析 先根据根与系数的关系求出x1+x2与x1•x2的值，再代入代数式进行计算即可．
解答 解：∵关于x的一元二次方程x2+2x-3=0的两根为x1，x2，
∴x1+x2=-2，x1•x2=3，
∴原式=2（x1+x2）+x1•x2=-4+3=-1．
故答案为：-1．
点评 本题考查的是根与系数的关系，熟知x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$是解答此题的关键．
练习册系列答案
相关题目
如图，已知AB为⊙O的直径，点D为半圆周上一点，且$\widehat{AD}$=2$\widehat{BD}$，则∠BOD=120°，∠AOD=60°．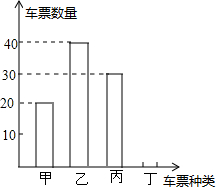
“五一”假期，成都某公司组织部分员工分别到甲、乙、丙、丁四地考察，公司按定额购买了前往各地的车票，如图是用来制作完整的车票种类和相应数量的条形统计图，根据统计图回答下列问题：
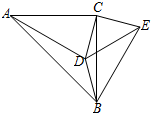如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE，则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是（ ）
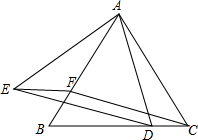如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF．