题目内容
14.问题提出平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.
初步思考
(1)如图①,在等边△ABC的内部和外部各作一个△ABC的巧妙点.(尺规作图,不写作法,保留作图痕迹)
(2)如图②,在△ABC中,AB=AC,∠BAC=36°,点D、E是△ABC的两个巧妙点,其中AD=AB,AE=AC,BD=BC=CE,连接DE,分别交AB、AC于点M、N.求证:DA2=DB•DE.
深入研究
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P可能为△ABC的巧妙点吗?若可能,请画出示意图,并直接写出∠BAC的度数;若不可能,请说明理由.

分析 (1)根据“巧妙点”的定义利用:点P在三角形的内部时,点P到△ABC的三个顶点的距离相等,所以点P是三角形的外心;点P在三角形的外部时,每条边的垂直平分线上的点只要能够使顶点这条边的两端点连接而成的三角形是等腰三角形即可;
(2)先证明△ADB≌△ABC,△ACE≌△ABC,得到相等的角,再证明∠BMD=∠ABD,得到DB=DM.最后证明△DAM∽△DEA,得到$\frac{DM}{DA}$=$\frac{DA}{DE}$,即DA2=DM•DE,由DM=DB,所以DA2=DB•DE.
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P能为△ABC的巧妙点,分别画出图形即可解答.
解答 解:(1)如图①;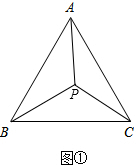
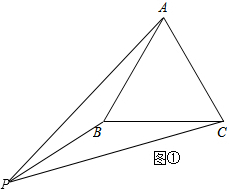
(2)∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
在△ADB和△ABC中
$\left\{\begin{array}{l}{AD=AC}\\{AB=AB}\\{DB=CB}\end{array}\right.$
∴△ADB≌△ABC,
同理:△ACE≌△ABC.
∴∠BAD=∠BAC=∠CAE=36°,∠ADB=∠ABD=∠ABC=72°,
∴∠DAE=∠BAD+∠BAC+∠CAE=108°,
∵AD=AB=AC=AE,
∴∠ADE=∠AED=36°=∠BAD,
∴∠BDM=∠BDA-∠MDA=36°,
∠BMD=∠ADM+∠DAM=72°=∠ABD,
∴DB=DM.
∵∠DBM=∠ABD,∠AED=∠BAD,
∴△DAM∽△DEA,
∴$\frac{DM}{DA}$=$\frac{DA}{DE}$,
∴DA2=DM•DE,
∵DM=DB,
∴DA2=DB•DE.
(3)
第一种如图①或图②(只需画一个即可),∠BAC=60°.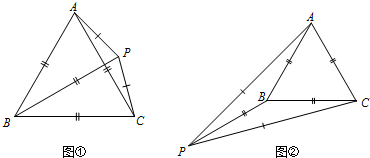
第二种如图③,∠BAC=36°;
第三种如图④,∠BAC=108°;
第四种如图⑤,∠BAC=120°.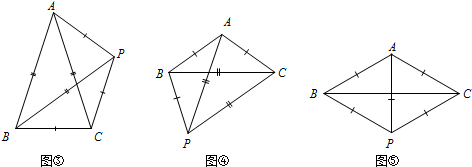
以上共四种:60°、36°、108°、120°.
点评 本题是三角形综合题,考查了等边三角形的性质、等腰三角形的性质,解决本题的关键是理解巧妙点的定义.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 能够完全重合 | B. | 三边对应相等 | ||
| C. | 两角及一边对应相等 | D. | 两边及一角对应相等 |
| A. | 1 | B. | -1 | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
| A. | x≥-1 | B. | x≠2 | C. | x≥-1且x≠2 | D. | 以上都不正确 |
 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )| A. | (-1,1) | B. | (-2,-1) | C. | (-3,1) | D. | (1,-2) |
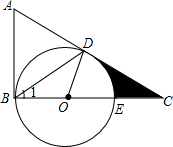 如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.