题目内容
2.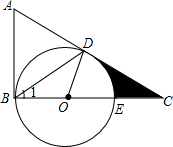 如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
分析 (1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;
(2)由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD=2$\sqrt{3}$,然后利用阴影部分的面积=S△COD-S扇形DOE和扇形的面积公式求解.
解答 (1)证明:∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
∵∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线;
(2)解:∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD=$\sqrt{3}$OD=2$\sqrt{3}$,
∴阴影部分的面积=S△COD-S扇形DOE
=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2π}{3}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了扇形面积的计算.

练习册系列答案
相关题目
12.若M-(-N)=0,则M与N的关系是( )
| A. | 互为相反数 | B. | 大小相等 | C. | M>N | D. | M<N |
17. 如图,将一条两边沿互相平行的纸带按图折叠,则∠α的度数等于( )
如图,将一条两边沿互相平行的纸带按图折叠,则∠α的度数等于( )
 如图,将一条两边沿互相平行的纸带按图折叠,则∠α的度数等于( )
如图,将一条两边沿互相平行的纸带按图折叠,则∠α的度数等于( )| A. | 50° | B. | 60° | C. | 75° | D. | 85° |
11.若关于x的一元二次方程x2-4x-k=0有两个实数根,则( )
| A. | k>4 | B. | k>-4 | C. | k≥4 | D. | k≥-4 |
12.为了解九(3)班学生每天零花钱的使用情况,小明随机调查了20名同学,结果如表:关于这20名同学每天使用的零花钱,下列说法错误的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 5 | 6 | 4 | 2 | 1 |
| A. | 众数是2元 | B. | 中位数是2元 | C. | 极差是5元 | D. | 平均数是2.45元 |
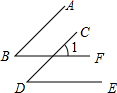 如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)
如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)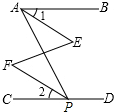 如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.
如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.